仕様限界内に収めるための因子設定 ~「シミュレーション実験」によるアプローチ~
JMPの「予測プロファイル」では、「満足度の最大化」を用いることで、各応答の目的(大きい方が良い・小さい方が良い・目標値に合わせる)をできるだけ同時に満たすような因子(説明変数)の組み合わせ、いわゆる最適条件を求められます。 ただし求められた因子の最適値は、あくまで1つの点であり、実際の工程では、温度や湿度などを最適値ぴったりに制御するのは難しく、さらに環境要因などにより、因子は最適値のまわりでばらつきをもって変動すると考えるのが自然です。 因子がばらつくのであれば、それに応じて応答もばらつくことになるので、応答の値も分布を構成します。もし応答に仕様範囲(LSL:下側、USL:上側)が設定されている場合、その分布の一部が仕様限界を超え、不適合が発生する可能性があります。 下図は、因子がばらつくことを想定したときの応答(Error1)の分布の例です。ヒストグラムを見ると、仕様範囲外に位置す...
 Masukawa_Nao
Masukawa_Nao

 John_Powell_JMP
John_Powell_JMP
 lkimhui
lkimhui
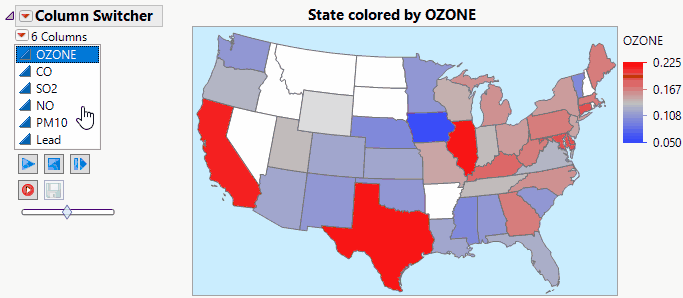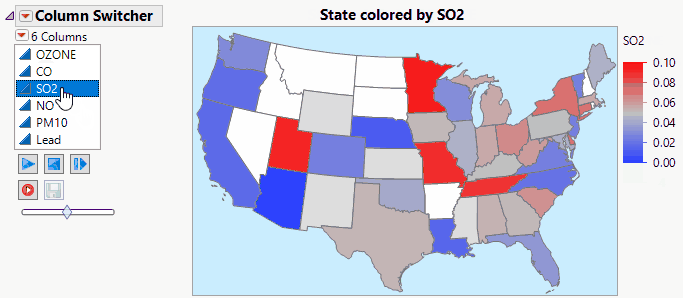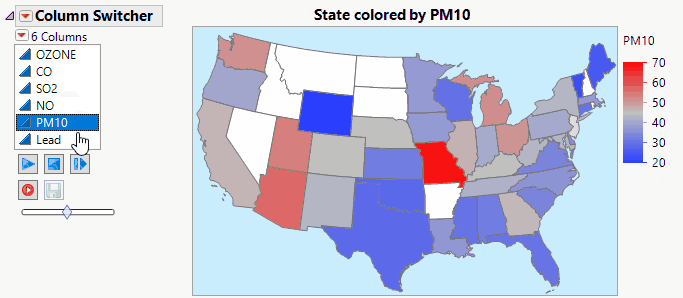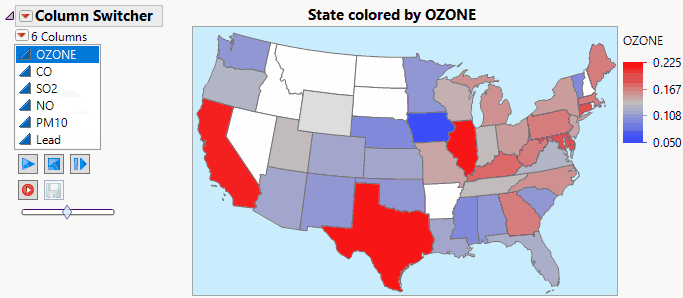

 Jed_Campbell
Jed_Campbell
 hannah_martin
hannah_martin
 Phil_Kay
Phil_Kay

 Victor_G
Victor_G

 Richard_Zink
Richard_Zink

 David_Elsheimer
David_Elsheimer

 scwise
scwise
 Craige_Hales
Craige_Hales

 Jeff_Perkinson
Jeff_Perkinson