このブログでは、経済や社会分野で所得や貯蓄の格差を分析する際に用いられる「ローレンツ曲線」と「ジニ係数」について説明します。併せてMLB(メジャーリーグベースボール)の各チームにおけるホームラン数の偏りを分析するために、JMPを用いてローレンツ曲線で視覚化し、ジニ係数で定量化した例を紹介します。
不平等さを測る指標:ジニ係数とローレンツ曲線
データの偏りや不平等を定量化する指標として、「ジニ係数」がよく知られています。そして、その不平等を視覚的に表現するために「ローレンツ曲線」が用いられます。
ジニ係数は「不平等の指標」とも呼ばれ、所得格差や教育格差など、さまざまな分野で格差の度合いを示す際に使われています。
下図は、家庭における所得格差を視覚化したローレンツ曲線(青色)です。横軸は家庭の累積割合、縦軸は累積所得割合を示します。所得格差がなく平等の場合、ローレンツ曲線は点線で示した45度線(「完全平等線」という)に一致します。一方、所得の格差が大きい、つまり不平等の場合、ローレンツ曲線は45度線から遠ざかります。
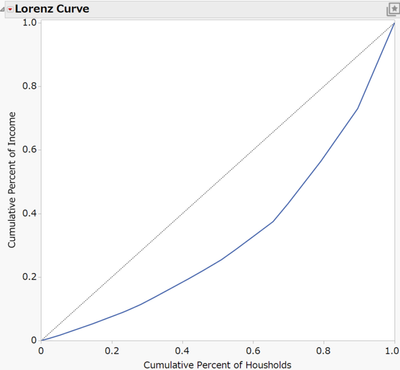
ローレンツ曲線とジニ係数との関係
ジニ係数は、ローレンツ曲線と完全平等線の間に囲まれた面積を基に計算されます。右下の直角三角形の面積を1としたときの囲まれた面積と定義され、次の式で求められます。
ジニ係数 = 1 - 2×(ローレンツ曲面下の面積)
完全に平等のときはローレンツ曲線が完全平等線に等しくなる、完全に不平等のときはローレンツ曲線が直角三角形になることから、ジニ係数は次のように解釈されます。
- ジニ係数が0:完全に平等(全員が同じ収入や資源を持つ)
- ジニ係数が1:完全に不平等(1人がすべてを独占している)
ちなみに日本の所得に関するジニ係数は、1990年:0.433、2003年:0.526、2021年:0.570 と年々上昇しています*。これらの数値は、日本で所得格差が拡大していることを示しています。
※ここで提示した数字は「当初所得ジニ係数」であり、税金や社会保険料を支払った後の所得を基準にした「再分配ジニ係数」とは異なります。
最初に述べたとおり、ローレンツ曲線やジニ係数は、経済や社会分野で用いられるケースが多いですが、それ以外の分野でも不平等さや偏りを測る指標として用いることができます。
そこで、今回はMLBのデータを使い、JMPでローレンツ曲線とジニ係数を求める例を紹介します。
ジニ係数の利用例:MLBのホームラン数の偏り
2024年のMLBレギュラーシーズンにおいて、ワールドシリーズおよびリーグチャンピオンシリーズに出場した4チームの打者のホームラン数の偏りを分析しました。
以下のヒストグラムは、各チームにおける打者のホームラン数の分布を示します。

野球に詳しい方であれば、Dodgersの外れ値(50-55本)、Yankeesの外れ値(55-60本)は誰だかわかりますよね?
Dodgersの例を用いて、JMPでジニ係数を計算し、ローレンツ曲線を作成する手順を以下に示します。
1. データの準備と計算式の作成
以下は、上記ヒストグラムの元となるデータであり、「Homeruns」(ホームランの本数)と「N」(人数)の列を含みます。これから計算式を用い、黄色で示した列を作成します。
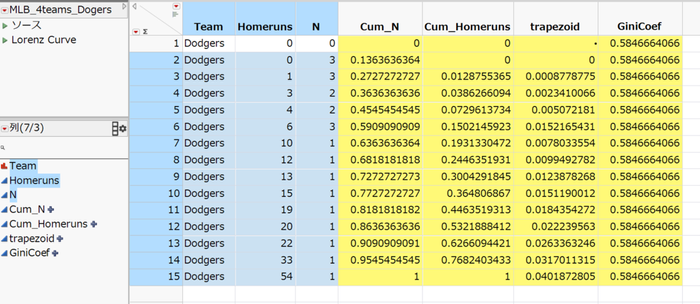
黄色の列は、それぞれ次の計算式を適用しています*。
- 列「Cum_N」: 人数の累積割合を示しています。ローレンツ曲線の横軸に用います。

- 列「Cum_Homeruns」:ホームランの累積割合を示しています。ローレンツ曲線の縦軸に用います。

- 列「trapezoid」:台形公式を用いてローレンツ曲面下の面積を計算しています。

- 列「GiniCoef」:台形の面積からジニ係数を計算しています。
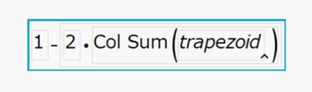
求められたジニ係数は、0.584です。
*これらの計算式をまとめて1つの式にすることもできますが、ここでは分かりやすさを優先し、あえて複数の列を用いて計算しています。
2. ローレンツ曲線の作成
新しく作成した列「Cum_N」、「Cum_Homeruns」を用い、「グラフビルダー」を使って折れ線グラフを作成します。
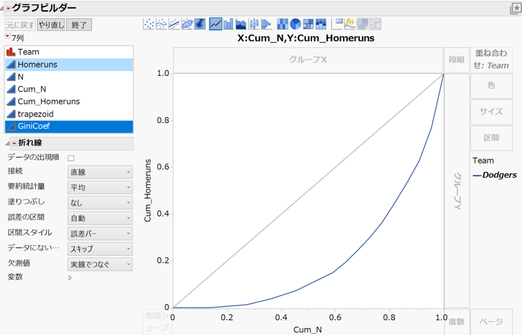
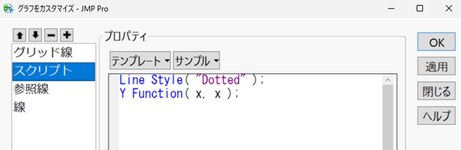
ここで、45度線(黒色の点線)はグラフ上で右クリックし、表示されるメニューから [カスタマイズ] を選択し、次のようなスクリプトを記述することにより表示できます。
Dodgersに加え、Yankees、Mets、Guardiansの3チームについても同様に計算し、ローレンツ曲線を重ね合わせた結果を以下に示します。
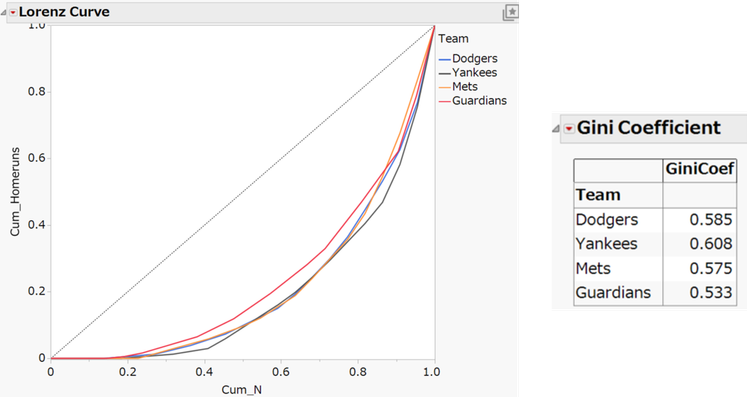
ローレンツ曲線では下側にたるんでいるほど、偏りが大きいことを示しています。ガーディアンズ(赤線)の偏りは他の3チームと比べて小さいことがわかります。併せてジニ係数を見ると、偏りが大きい順にDodgers、Yankees、Mets、Gardiansとなっています。
ワールドシリーズに進出したDodgers、Yankeesは、一部の選手が圧倒的に多くのホームランを打っており、それが偏りの大きな要因です。
本ブログでは、ジニ係数とローレンツ曲線を使い、MLBのホームラン数の偏りを視覚化・定量化する例を示しました。この手法は、経済や社会分野だけでなく、スポーツやその他の分野のデータ分析にも応用できます。
4つのチームに対するジニ係数を算出したJMPのデータテーブルは、本ブログに添付していますのでご参考にお願いします(MLB2024_4teams.jmp)。
by 増川 直裕(JMP Japan)
Naohiro Masukawa - JMP User Community
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.