Screening for safety signals among recurrent adverse events with the max difference plot
I introduce the max difference plot as a more useful alternative to the tendril plot when screening for notable safety signals among recurrent adverse events.
 Richard_Zink
Richard_Zink

 MaddiWalsleben
MaddiWalsleben
 Masukawa_Nao
Masukawa_Nao
 anne_milley
anne_milley
 Dahlia_Watkins
Dahlia_Watkins

 Craige_Hales
Craige_Hales


 John_Powell_JMP
John_Powell_JMP
 lkimhui
lkimhui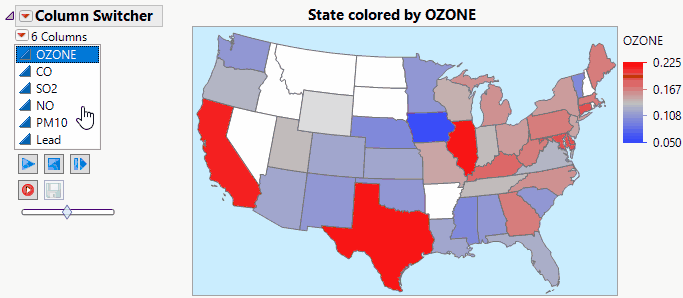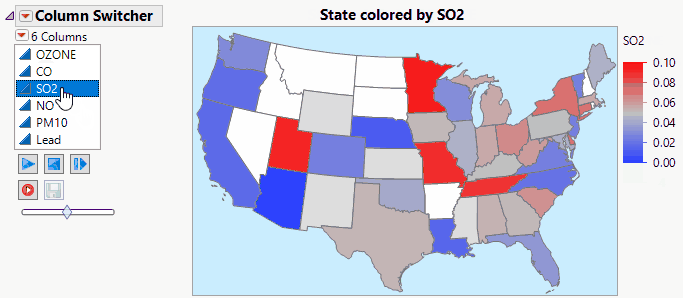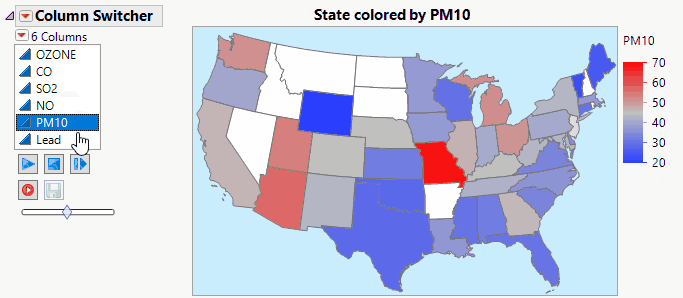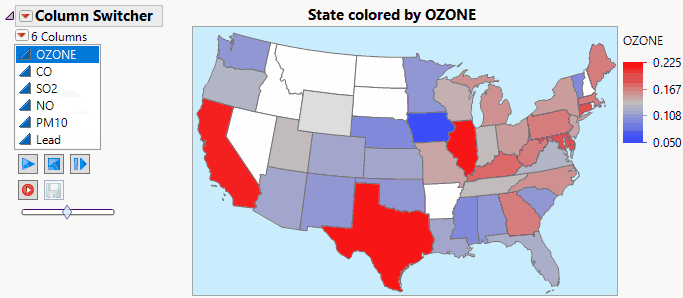

 Jed_Campbell
Jed_Campbell
 hannah_martin
hannah_martin
 Phil_Kay
Phil_Kay

 Victor_G
Victor_G
