近年のJMPのバージョンアップ において、最新版のJMP 18ではt検定における効果量「Cohenのd」(Cohen's d)を、JMP 17以降では回帰分析における効果量「η2」(イータ2乗)、「ω2」(オメガ2乗)を出力できるようになりました。
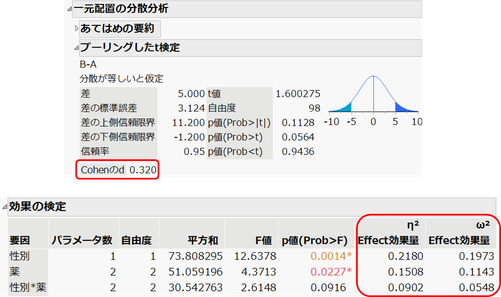
効果量とは、統計モデルにおける説明変数(要因)が目的変数に与える影響の大きさを示す指標です。要因が(偶然ではなく)目的変数に影響を与えているかを示す指標としてp値がありますが、これは統計的な有意性を判断するものであり、効果の大きさを示すものではありません。
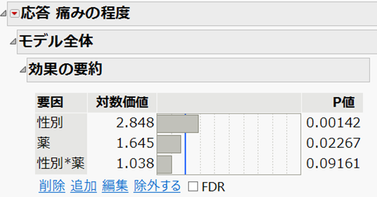
JMPでは「モデルのあてはめ」のレポートとして、以下の「効果の要約」が表示されます。このレポートでは、p値が小さい順(対数価値が大きい順)に並びますが、これは性別、薬、性別*薬の順に効果が大きいことを直接示すわけではありません。あくまで統計的な有意性の大きさを示しています。
本ブログでは効果量の意味、JMPでの出力方法、計算式、指標の目安について説明します。
t検定の効果量:「Cohenのd」 (Cohen's d)
Cohenのd 統計量は、t検定の効果量として用いられます。すなわち等分散性を仮定し、2つのグループ間の平均値を比較するときです。
シミュレーションデータでの説明
2つのグループ(A、B)の血糖値(mg/dl)を比較するシミュレーションデータを作成します。
グループA : N(105, 152) からランダムに抽出したサンプル
グループB : N(110, 152) からランダムに抽出したサンプル
N(μ、σ2) は、平均μ、標準偏差 σ に従う正規分布を示します。
このとき、グループA、Bからそれぞれ50個のサンプルを抽出してt検定を実施したときの結果(左図)、グループA、Bからそれぞれ250個サンプルを抽出してt検定を実施したときの結果(右図)を示します。
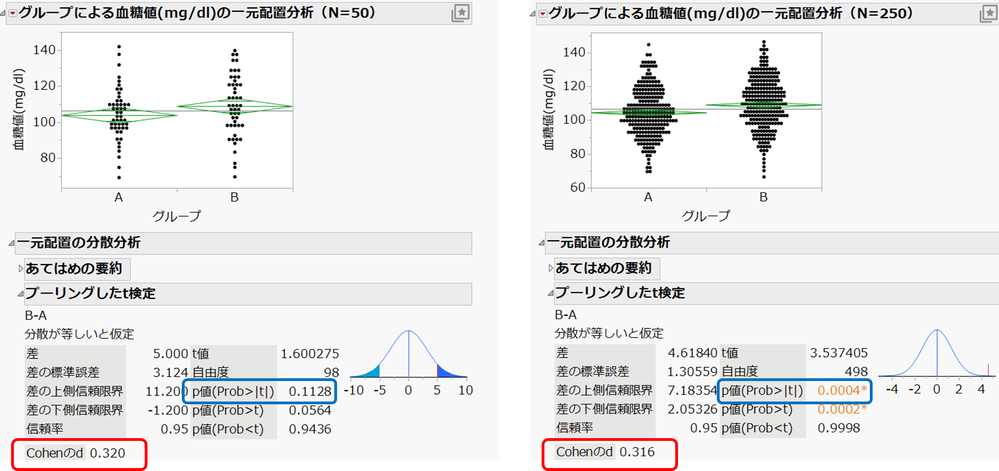
双方のレポートについて両側検定のp値を参照すると、N=50のときはp = 0.1128、N=250のときは p=0.0004 です。有意水準α = 0.05 とすると、前者は有意ではなく、後者は有意となります。
このシミュレーションデータでは、Aの平均が105、Bの平均が110のため、平均に5の差があるのですが、N =50ではサンプル数が少ないために差が検出できず、N=250ではサンプル数が増えたので有意差が検出できたことを示しています。
p値はサンプルサイズが大きい場合、少しの差であっても小さくなる傾向があるため、効果の大きさを確認するには、Cohenのdを用います。
JMPでの操作(JMP 18)
- [分析] > [二変量の関係]を選択。Yに連続尺度、Xに名義(順序)尺度を指定して「一元配置分散分析」のレポートを表示します。
- レポート左上の赤い三角ボタンから [平均/ANOVA/プーリングしたt検定] を選択します。
⇒ 「プーリングしたt検定」のレポート左下に「Cohenのd」のレポートが出力されます。
この値を参照すると、N=50のときとN=250のときで値がほぼ等しくなっています(0.32程度)。双方の効果の大きさはほぼ等しいと考えられますが、効果量はサンプルサイズによらず推定されていることを示しています*。
*Nが大きいほど、効果量の推定精度は高まります。
計算式
Cohenのdは、次の式で算出できます。
d = (Bグループの平均 - Aグループの平均)÷ プールされた標準偏差
プールされた標準偏差は誤差の標準偏差(RMSE)と同じです。
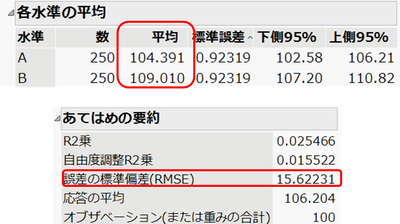
計算例:N =250のときのレポートに表示される上記の値を用い、次のように計算できます。
d = (109.010 - 104.391 ) ÷ 15.622 = 0.316
効果の大きさの目安
あくまでも目安ですが、Cohenのdでは次のような基準が用いられています。
0.2未満:効果がない、0.2~0.5 :効果が小さい
0.5~0.8:効果が中程度、0.8以上:効果が大きい
注意:JMPではグループ変数について、後の水準 - 前の水準 の差を比較します。この例では最初の水準がA、後の水準がBのため、B の平均 - Aの平均を比較しています。
回帰分析の効果量:η2、ω2
JMP 17以降では「モデルのあてはめ」で手法を「標準最小2乗」として回帰モデルをあてはめた際、「効果の検定」レポートに、効果量η2、ω2を表示できます。
以下の例は、JMPのサンプルデータ「Analgesics.jmp」において、痛みの程度を[Y]に、性別、薬、性別*薬を[モデル効果の構成]に指定したときのレポートについて効果量を表示しています。
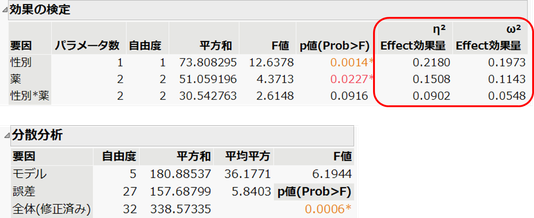
η2、ω2は分散分析における効果量として知られていますが、説明変数が連続のときの線形モデルにも適用できます。
JMPでの操作(JMP 17以降)
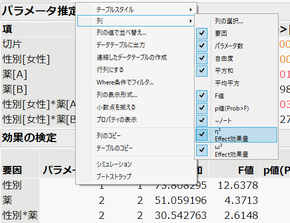
「モデルのあてはめ」のレポート「効果の検定」において、統計量部分を右クリックして表示されるメニューから [列] > [η2]、または [ω2]を選択します。
計算式
η2やω2は、その要因で全体の分散をどれぐらい説明できているかを示す指標です。例えば、性別の効果量は次の式で算出されます。
性別のη2 = 性別の平方和 ÷ 全体(修正済み)の平方和
= 73.808 ÷ 338.573 = 0.218
全体の分散(平方和)を、性別でどれぐらいの割合を説明できているかを示しています。0.218ということは、性別がYの分散の21.8%説明していることを示します。
η2は計算が簡便で分かりやすい指標ですが、それをバイアス補正したものがω2です。計算式は省略しますが、こちらも「効果の検定」や「分散分析」に表示される統計量から計算できます。
効果の大きさの目安
η2、ω2の値の目安は、効果量小:0.01、効果量中: 0.06、効果量大:0.14 といったものが提唱されていますが、こちらもあくまでも目安です。
まとめ
統計的有意性とp値に関するASA声明(The ASA Statement of Statistical Significance and P-Values)(日本生物統計学会が日本語訳を作成)では、「科学的な結論や、ビジネス、政策における決定は、P 値がある値(訳注: 有意水準)を超えたかどうかにのみ基づくべきではない。」という記載があります。
近年、学術論文ではp値のほかにも、信頼区間や効果量の記載が求められることが増えてきています。
今回紹介した効果量は、仮説検定以外の評価の方法の一つとして覚えておくとよいでしょう。
by 増川 直裕(JMP Japan)
Naohiro Masukawa - JMP User Community
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.