問題背景
產品的耐用性顯然是對最終用戶和製造商都非常重要的品質特性。對於最終用戶來說,手機的耐用性尤為重要。例如,手機掉落在硬物上可能會導致螢幕破裂甚至破碎,使手機無法使用。為了評估這些螢幕的耐用性,製造商對一批螢幕進行了多種測試,以類比使用者的典型磨損情況,例如將手機掉落在混凝土表面上。
一家螢幕製造商的材料科學家一直在試驗兩種新的鋁矽酸鹽玻璃配方。這兩種配方是透過修改材料成分和固化過程製成的。為了簡化,我們將這兩種配方分別稱為螢幕類型A和B。
為了測試,開發了每種類型的10塊螢幕樣本。每塊螢幕都安裝在相同型號的手機上。然後,這些手機以控制一致的方式從1米高度掉落到混凝土表面。記錄了二元變數“成功”(無損傷)和“失敗”(螢幕損傷)。
公司的目標之一是97%的螢幕製造出來能夠承受1米高度的跌落而不受損傷(即總體成功率)
任務
工程團隊希望透過資料解答兩個主要問題:
- 是否有足夠的統計證據得出結論,每種螢幕類型在1.0米高度跌落時的成功率至少為97%?
- 是否有統計證據得出結論,其中一種螢幕類型的成功率比另一種更好?
數據
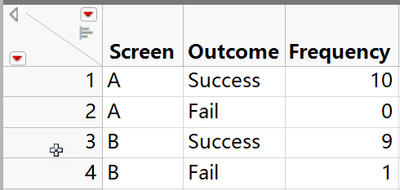
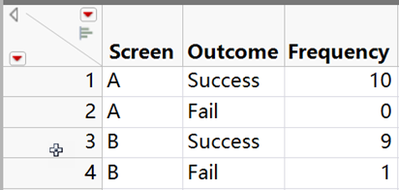
資料存儲在結果/頻率表格格式中。
螢幕 兩種螢幕類型(A,B)
結果 兩種結果(成功,失敗)
頻率 導致成功或失敗的手機數量
分析
總體比例的信賴區間
我們首先使用分佈平臺以圖形方式總結資料。圖1顯示了橫條圖,以及兩種螢幕類型每種結果的計數和比例。
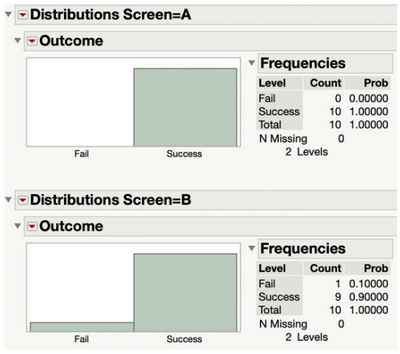

圖1 分佈
要創建,選擇分析>分佈。選擇結果作為Y變數,頻率作為頻率變數,螢幕作為依據變數。
所有10部帶有螢幕類型A的手機(100%)都沒有經歷螢幕損壞,而10部帶有螢幕類型B的手機中有一部(10%)發生了損壞。由於這只是對20部手機進行的測試結果,因此我們不應立即得出結論認為螢幕A通常比B更好,而應進行更正式的統計分析。
因為這些結果可能發生在這樣的測試中,如果事實上兩種螢幕類型之間的總體成功率是相同的。我們的分析將允許我們量化這種可能性。我們還將能夠估計每種螢幕類型的總體成功率,並附帶統計不確定性的度量。
我們將透過首先計算每種螢幕類型的總體成功率的95%信賴區間估計來開始這一分析。信賴區間透過基於僅一個樣本提供一個參數的可能值範圍來估計總體參數。
圖 2 顯示了基於這些資料的信賴區間。


圖2 分佈和信賴區間
要創建,請從每種螢幕類型的橫條圖旁邊的紅色三角形中選擇信賴區間 為0.95。
這些區間的解釋如下:我們有95%的把握認為螢幕類型A在1米跌落高度的總體成功率介於72.2%至100%之間,而我們有95%的把握認為螢幕類型B在1米跌落高度的總體成功率介於59.6%至98.2%之間。信賴區間量化了估計中的統計不確定性。由於樣本量較小(每種螢幕類型10部手機),不確定性相當大,這反映在信賴區間的寬度上(螢幕類型A為100 – 72.7 = 27.3,螢幕類型B為98.2 – 59.6 = 38.6)。
技術說明:圖2 中顯示的信賴區間和下一節中進行的假設檢驗都基於使用二項分佈的統計程式。用於估計總體比例的另一種常見方法是基於常態分佈。使用該技術的結果將與此處顯示的結果不同。
為了在95%的信賴水準上統計證明所需的97%總體成功率,信賴區間的下限需要超過97%,這意味著我們估計成功率的任何可能值都大於97%。在我們的資料中,螢幕A的下限是72.2%,螢幕B是59.6%。顯然,我們沒有產生統計證據來證明成功率超過97%。事實上,這些信賴區間中的誤差幅度揭示了,基於僅測試10部手機,不可能在95%的信賴水準上證明這種成功率水準。即使對於螢幕類型A的完美結果,我們也只能估計總體成功率最高為72.7%。我們需要測試足夠多的手機,才能產生一個誤差幅度更小的信賴區間,例如97.5% - 100%的信賴區間。
單比例的假設檢驗
由於信賴區間表明所期望的97%總體成功率的標準未達到,因此無需進行假設檢驗,因為它將得出相同的結論。我們仍將進行假設檢驗,以說明如何進行並解釋輸出。
我們可以將感興趣的假設表述為:
H0: PA≤0.97
HA: PA>0.97
H0: PB≤0.97
H0: PB>0.97
分別是每種螢幕類型的總體成功率。
圖 3 顯示了添加到分佈輸出中的假設檢驗結果。


圖 3 分佈和假設檢驗
要創建,請從每種螢幕類型的橫條圖旁邊的紅色三角形中選擇測試概率。輸入0.97作為成功的假設概率。選擇大於假設值的概率(精確的單側二項式檢驗)。
兩個測試的p值都很大(螢幕A為0.7374,螢幕B為0.9655),表明,正如我們已經確定的,沒有統計證據表明達到了所期望的97%成功率,我們選擇的顯著為0.05。
重要的是,我們的結論不應認為目前的分析已經產生了統計證據表明螢幕不符合標準。相反,我們沒有產生統計證據來得出他們確實如此的結論。也許如果測試了更多螢幕,我們將能夠產生必要的證據。
兩個比例之間的差異的信賴區間和假設檢驗
跌落測試的另一個目標是評估是否有統計證據得出結論,兩種螢幕類型的成功率不同。注意信賴區間的重疊有多大:螢幕A為[72.2% - 100%],螢幕B為[59.6% - 98.2%]。由此我們可以看出,沒有足夠的統計證據得出結論,兩種螢幕類型的成功率之間存在差異。再次,這可能是因為測試的螢幕數量少的結果;測試更多螢幕可能會產生證明差異的必要統計證據。
儘管如此,我們將展示在比較兩個總體比例時通常進行的統計分析類型,因為在練習中將要求您使用更多測試的手機進行這些分析。將演示五種不同的統計技術:
- 列聯表分析
- 雙樣本比例的假設檢驗
- 兩個比例差異的信賴區間估計
- 相對風險的信賴區間估計
每項分析都將得出相同的結論:沒有足夠的統計證據來得出兩種螢幕類型之間成功率有差異的結論。前三種假設檢驗可以寫為:
H0: PA=PB
HA: PA≠PB
或等效地
H0: PA-PB=0
HA: PA-PB≠0
其中PA和PB分別是螢幕類型A和B的總體成功率。
圖4是來自列聯表分析的輸出。


為了創建這個,選擇分析>以X擬合Y。將結果放在Y,回應中,螢幕放在X,因數中,頻率放在頻數中。右擊馬賽克圖表並選擇在儲存格標記下的百分比標籤。列聯表輸出中的紅色三角形提供了顯示在表格儲存格中的資訊的選擇。
似然比和皮爾遜的p值顯示0.2303和0.3049,正如預期的那樣,沒有足夠的統計證據表明兩種螢幕類型之間的總體成功率有差異。
圖5包含了兩樣本比例檢驗的結果,這是另一種測試假設的方法。如果有超過兩個類別(例如,螢幕類型C,D等),則可以使用列聯表分析中的卡方檢驗,而當只有兩個組時,只有兩樣本比例檢驗可用,就像這裡的情況一樣。

要創建,請從頂部紅色三角形中選擇“雙樣本比例檢驗”。
如預期的那樣,這種統計分析技術的p值很大(0.5338),表明沒有統計證據表明兩種螢幕類型之間的成功率有差異。同時請注意,PA - PB(總體成功率的差異)的信賴區間是[-.018, 0.346]。這被解釋為:我們有95%的信心估計螢幕類型A的總體成功率比螢幕類型B的總體成功率小0.18個單位,高達0.346個單位。也就是說,我們估計螢幕類型A的總體成功率可能比螢幕類型B的總體成功率小,也可能比螢幕類型B的總體成功率大。如果區間完全大於0或小於0,才會在所選的信賴水準上存在統計上顯著的證據。這個信賴區間顯示0是PA - PB的一個合理值。換句話說,成功率之間沒有差異。
相對風險的信賴區間
進行兩樣本比較分析的第四種方法是透過檢查稱為相對風險的成功率比率。這種比率的假設檢驗框架可以寫為:其中PA和PB分別是螢幕類型A和B的總體成功率。
H0: PA/PB=1
HA: PA/PB≠1
這種方法將感興趣的參數表述為兩個成功率之間的百分比增減而不是它們之間的差異。這是描述兩個比例之間差異的一種有用的方式。
圖6顯示了該分析的結果。

為了創建這個,從頂部的紅色三角形中選擇相對風險。選擇所需的回應結果和分子中的類別。
信賴區間[0.904, 1.366]被解釋為:我們有95%的信心估計螢幕類型A的總體成功率是螢幕類型A的總體成功率的90.4%到136.6%之間。也就是說,螢幕類型A的總體成功率可能比螢幕類型B的總體成功率小,也可能比螢幕類型B的總體成功率大。只有當相對風險的信賴區間估計完全大於1或小於1時,才會在所選的信賴水準上存在統計上顯著的證據。這個信賴區間顯示1是PA / PB的一個合理值。換句話說,成功率之間沒有差異。
統計洞察
我們的分析表明,資料中沒有統計證據來證明所需的97%總體成功率。我們也沒有產生任何統計證據來得出兩種螢幕之間總體成功率有差異的結論。正如之前所述,我們不應該得出我們的分析已經產生了統計證據表明螢幕不符合所需成功率的結論;而是我們沒有產生統計證據來得出他們確實符合的結論。同樣,我們沒有產生統計證據來得出兩種螢幕類型具有相同成功率的結論,只是我們還沒有產生統計證據說它們不同。更多的測試可能能夠產生這些證據。
本篇文章案例源自《Durability of Mobile Phone Screen - Part 1 | JMP》
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.