JMPのボルケーノプロットで重要要因を直感的に深掘りする(操作動画あり)
下のグラフは火山が噴火しているように見えることから、ボルケーノプロット(Volcano Plot)と呼ばれています。 もともと遺伝子解析の分野で用いられているプロットで、多数の遺伝子発現量をグループ間(例:性別や遺伝子型など)で比較する際に、差の大きさと有意性を同時に可視化するために使用されます。 ただし、遺伝子解析に限らず、多数の変数の中から重要なものを効率的にスクリーニングする用途でも利用できます。例えば、工程データにおいて、改善前と改善後の多くのパラメータを比較し、影響の大きい工程を抽出するといった場面でも有効です。 ボルケーノプロットは、差の大きさと有意性という統計量を2次元上に表現したグラフですが、JMPではグラフ上から直接データを深掘りできるため、スクリーニング作業を効率化できます。 また JMP 19 では、ボルケーノプロットに関する新機能も追加されています。本記事では、そ...
 Masukawa_Nao
Masukawa_Nao

 Craige_Hales
Craige_Hales


 John_Powell_JMP
John_Powell_JMP
 lkimhui
lkimhui
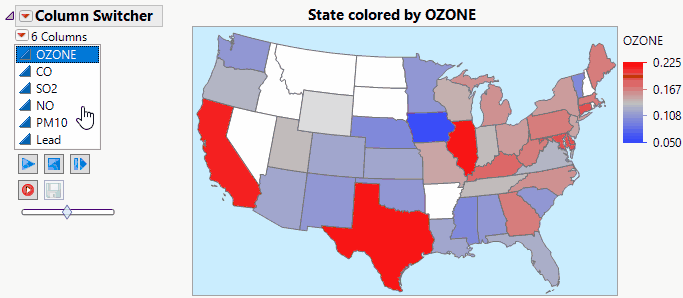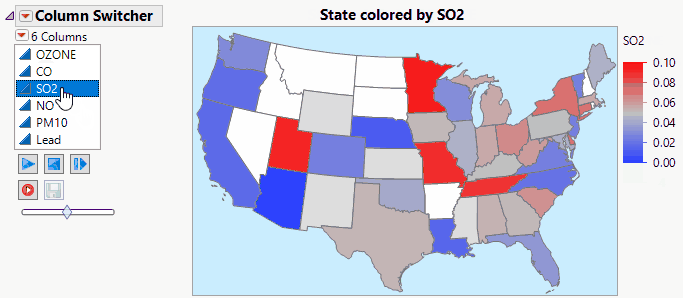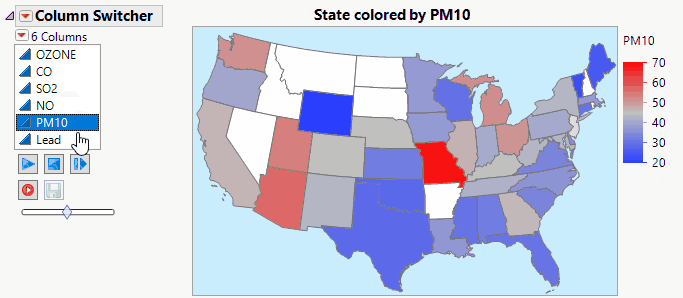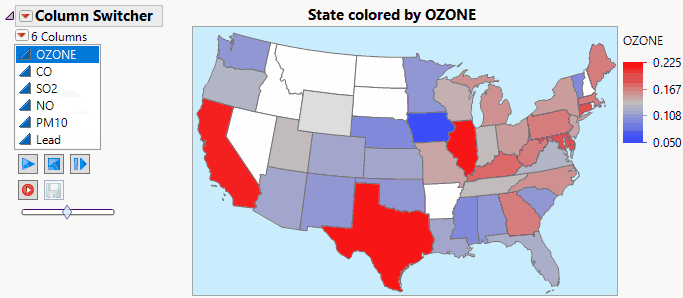

 Jed_Campbell
Jed_Campbell
 hannah_martin
hannah_martin
 Phil_Kay
Phil_Kay

 Victor_G
Victor_G

 Richard_Zink
Richard_Zink

 David_Elsheimer
David_Elsheimer

 scwise
scwise