Hoping your products are too good to fail? Find out using JMP® 18 Constant Stress Accelerated Life Test (CSALT)
To predict the reliability of some parts or products, the time and resources required to test under normal conditions isn’t practical, because it could take years for a failure to occur. Instead, eng...
 gail_massari
gail_massari
 Peter_Hersh
Peter_Hersh
 Masukawa_Nao
Masukawa_Nao
 Jed_Campbell
Jed_Campbell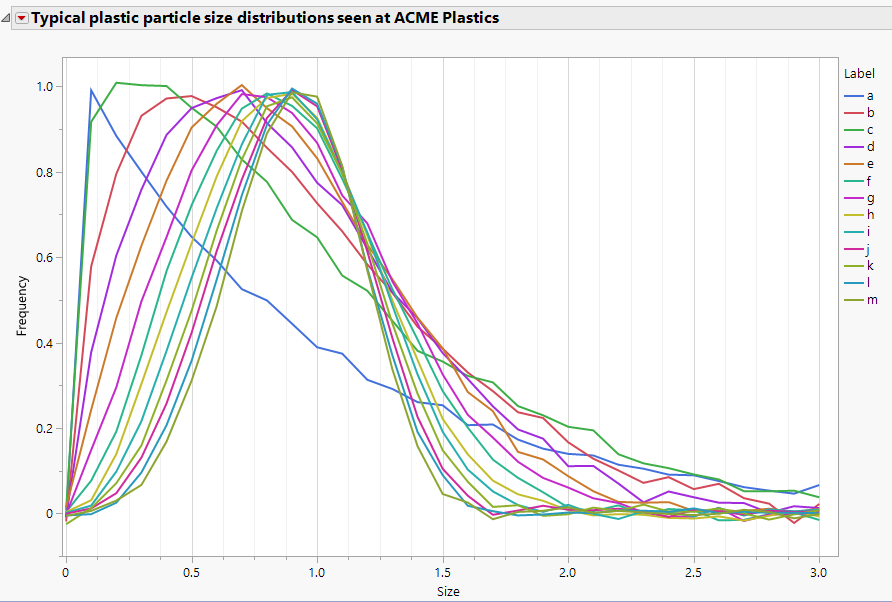
 Phil_Kay
Phil_Kay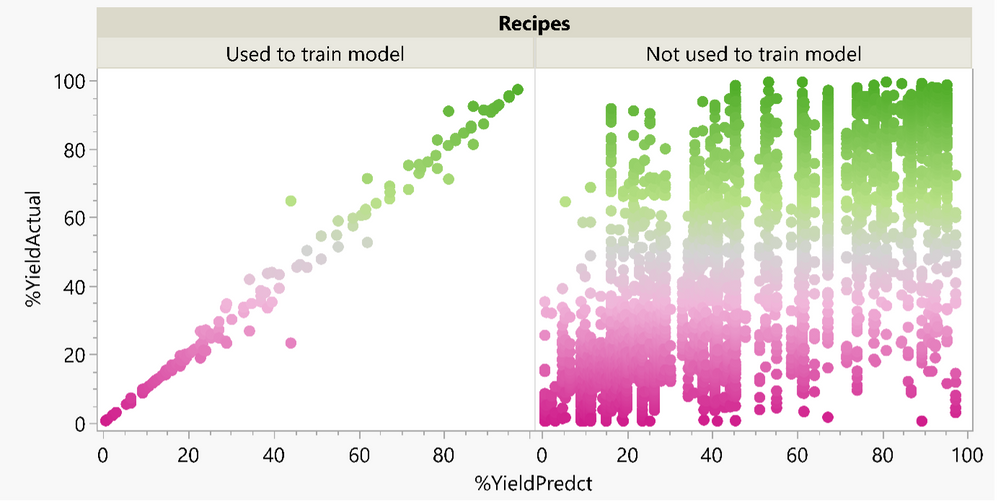
 Bill_Worley
Bill_Worley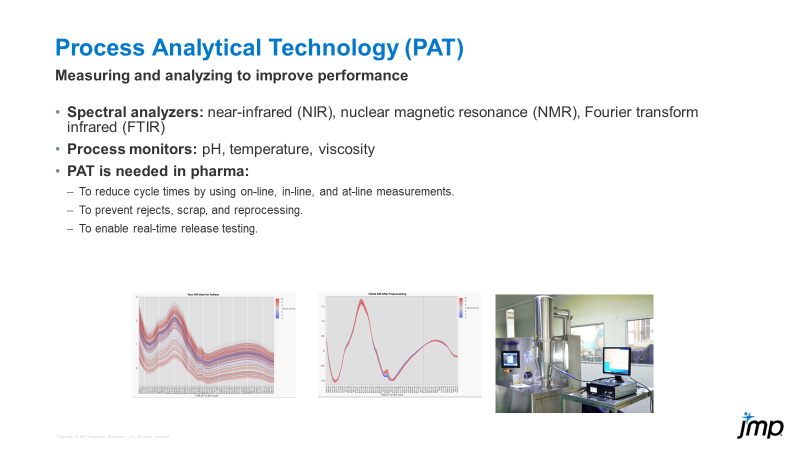
 DaeYun_Kim
DaeYun_Kim
 SamGardner
SamGardner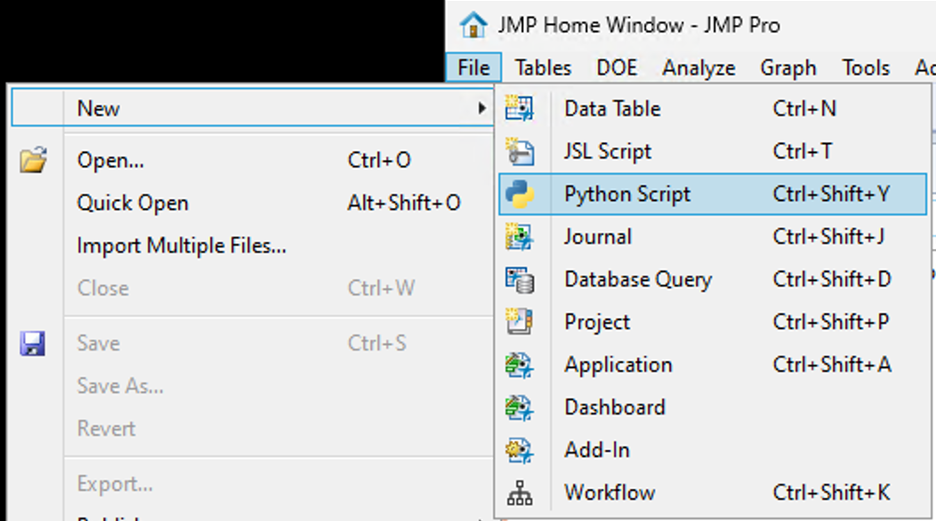

 Valerie_Nedbal
Valerie_Nedbal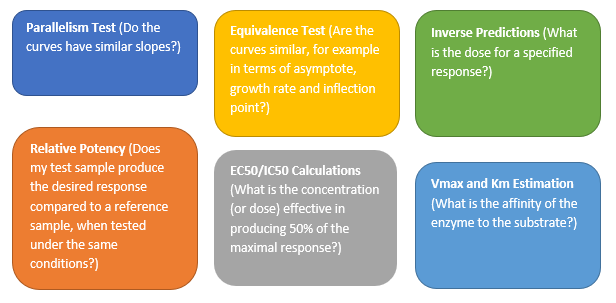
 Richard_Zink
Richard_Zink
 KristenBradford
KristenBradford
 Chris_Kirchberg
Chris_Kirchberg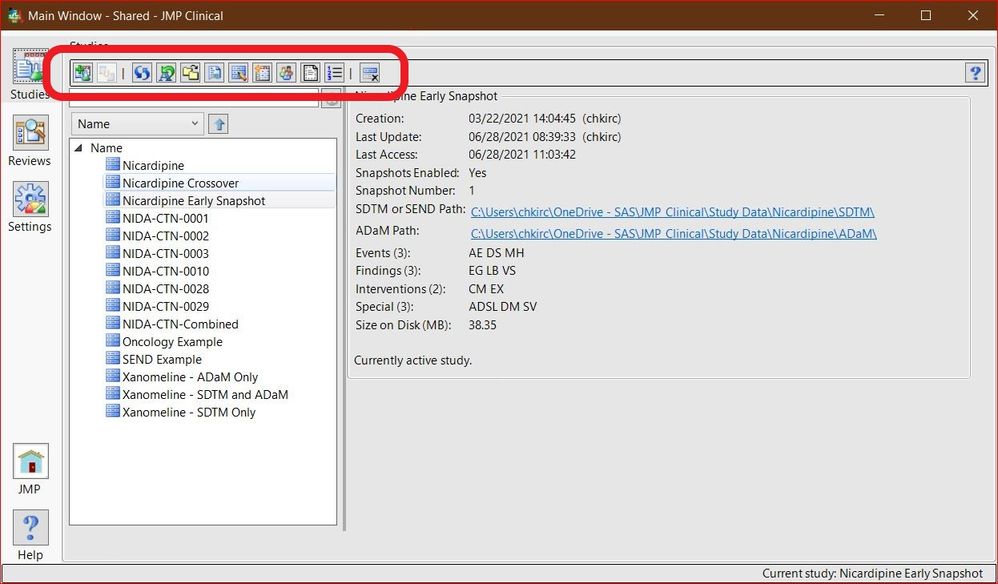
 cweisbart
cweisbart
 Paul_Nelson
Paul_Nelson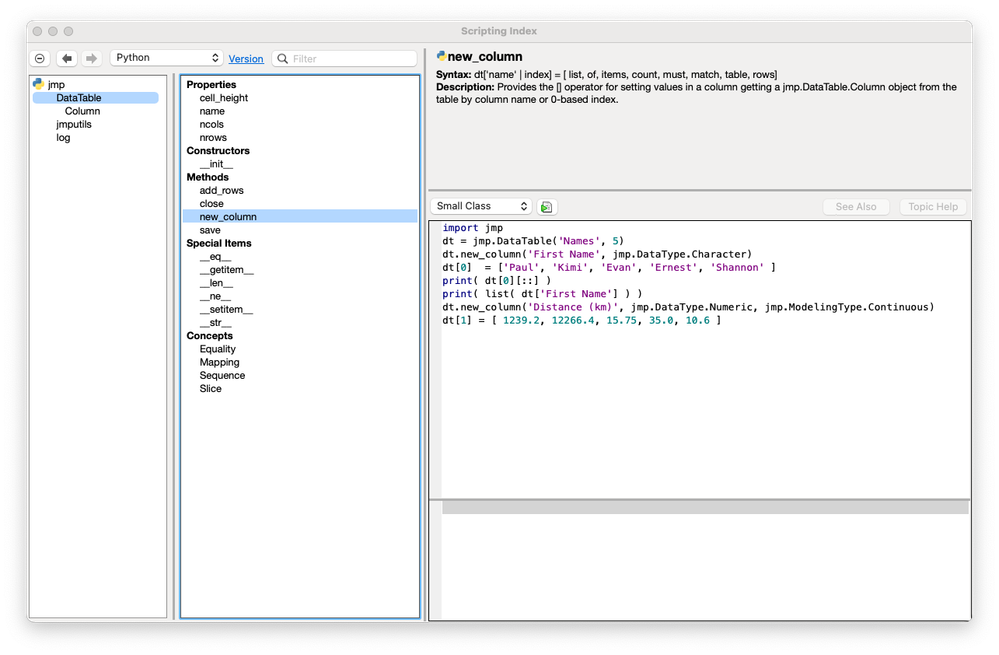
 Craige_Hales
Craige_Hales
 anne_milley
anne_milley
 Di_Michelson
Di_Michelson
 JohnPonte
JohnPonte