Draft day derby: The wild world of picking an NFL quarterback
The 2024 NFL draft begins Thursday, April 25, and will be full of intrigue for NFL fans. For teams near the bottom of the standing, the draft represents hope for the future. The right player can turn...
 Peter_Hersh
Peter_Hersh

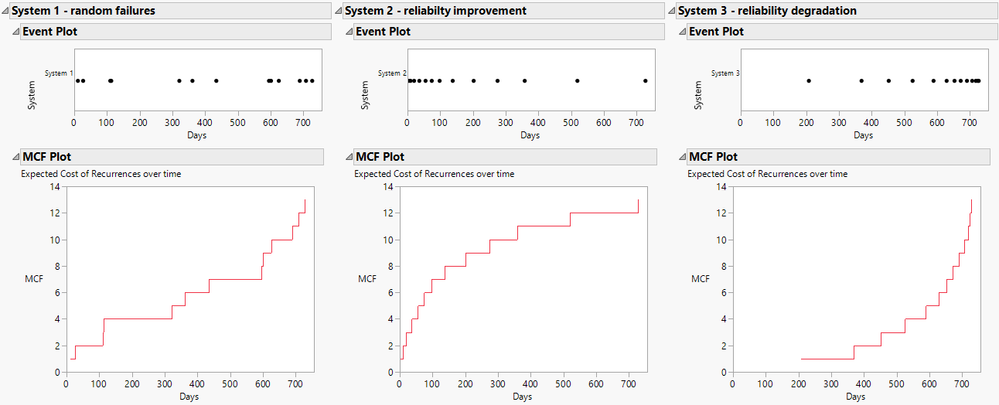
 Masukawa_Nao
Masukawa_Nao
 Paul_Nelson
Paul_Nelson
 gail_massari
gail_massari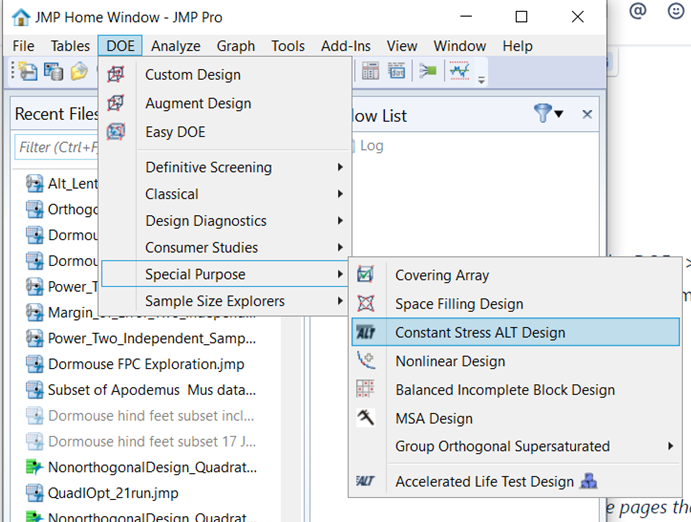

 Jed_Campbell
Jed_Campbell
 Phil_Kay
Phil_Kay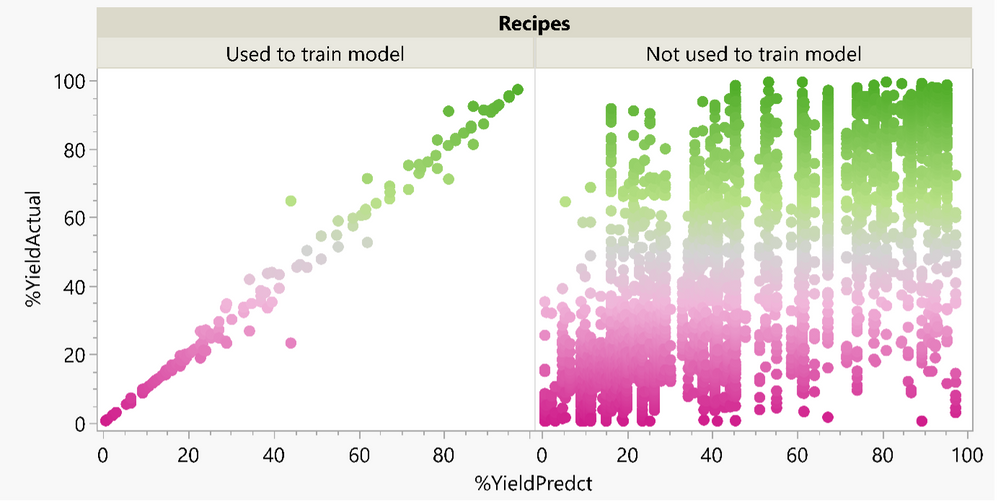
 Bill_Worley
Bill_Worley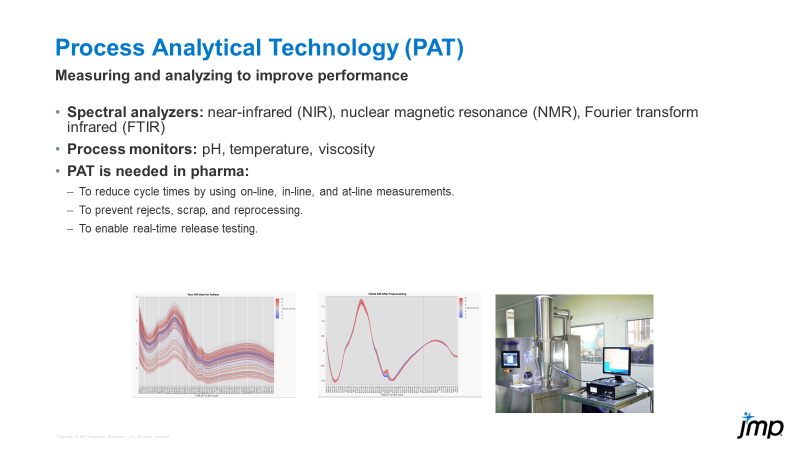
 DaeYun_Kim
DaeYun_Kim
 SamGardner
SamGardner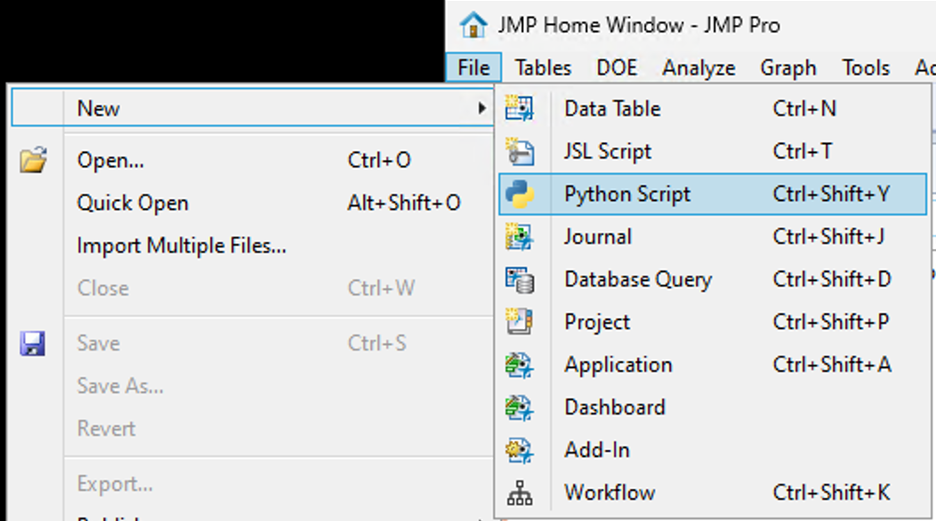

 Valerie_Nedbal
Valerie_Nedbal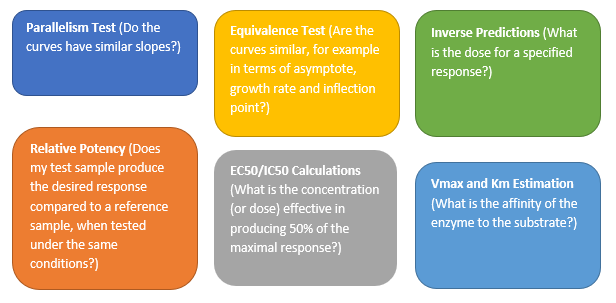
 Richard_Zink
Richard_Zink KristenBradford
KristenBradford
 Chris_Kirchberg
Chris_Kirchberg
 cweisbart
cweisbart
 Craige_Hales
Craige_Hales
 anne_milley
anne_milley
 Di_Michelson
Di_Michelson