Double your fun with double forest plots!
We explore Happy Little Forests, a happy little JMP add-in for producing many types of forest plots.
 Richard_Zink
Richard_Zink
We explore Happy Little Forests, a happy little JMP add-in for producing many types of forest plots.
 Richard_Zink
Richard_Zink

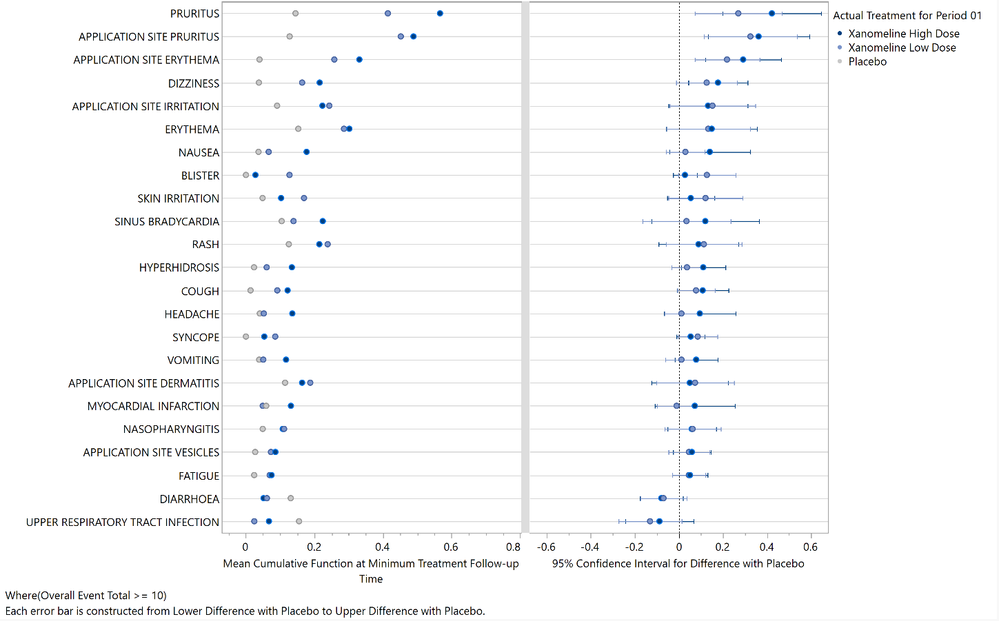
I introduce the max difference plot as a more useful alternative to the tendril plot when screening for notable safety signals among recurrent adverse events.
 Richard_Zink
Richard_Zink
Discover how JMP Tech Support goes beyond problem-solving to help you learn, explore, and succeed with confidence in 2026.
 MaddiWalsleben
MaddiWalsleben

医薬品開発において「溶出試験」とは、薬が体の中でどのような挙動を示すかを、試験管内で調べる試験のことを指します。 例えばジェネリック医薬品では、有効成分は同じでも、添加物や製造方法などの処方が変更されることがあります。その際、一定時間ごとに溶出率(有効成分が溶け出した割合)を測定し、変更前の製剤と変更後の製剤を比較して、溶出の傾向が類似していることを示す必要があります。 下図は、横軸を時間(分)、縦軸を溶出率とした、溶出曲線と呼ばれるものです。pH4.5、pH6.0、または水(Water)を試験液として用いた場合について、試験製剤(Test)と標準製剤(Reference)の時間ごとの溶出率をプロットし、折れ線で結んでいます。 *実際にY軸にプロットされている点は、複数のサンプル製剤の溶出率の平均値となります。 3種類の試験液における2つの曲線を比較すると、時間とともに溶出率が上昇し、1...
 Masukawa_Nao
Masukawa_Nao

“We have been raised on a steady diet of mixed messages regarding failure.”
 anne_milley
anne_milley

Is a data connector always necessary? Data connectors are an exciting addition to JMP, but they are not always necessary in every instance. This article discusses each data connector type within the new data connector framework to help you determine the best method for accessing your data.
 Dahlia_Watkins
Dahlia_Watkins

下のグラフは火山が噴火しているように見えることから、ボルケーノプロット(Volcano Plot)と呼ばれています。 もともと遺伝子解析の分野で用いられているプロットで、多数の遺伝子発現量をグループ間(例:性別や遺伝子型など)で比較する際に、差の大きさと有意性を同時に可視化するために使用されます。 ただし、遺伝子解析に限らず、多数の変数の中から重要なものを効率的にスクリーニングする用途でも利用できます。例えば、工程データにおいて、改善前と改善後の多くのパラメータを比較し、影響の大きい工程を抽出するといった場面でも有効です。 ボルケーノプロットは、差の大きさと有意性という統計量を2次元上に表現したグラフですが、JMPではグラフ上から直接データを深掘りできるため、スクリーニング作業を効率化できます。 また JMP 19 では、ボルケーノプロットに関する新機能も追加されています。本記事では、そ...
 Masukawa_Nao
Masukawa_Nao

This post shows a way-too-slow way to do ray marching and a perfectly fine Python way to make an animated WebP (like an animated Gif, but so much nicer!) Part 1: file formats This JSL uses the Python PIL library to make some test files to compare size, speed, and quality of PNG, JPEG, and WebP files. GIF is in part 2. If you want to run it, use 0 or 1 on the second line to make each picture. Th...
 Craige_Hales
Craige_Hales

以下のデータは、各国の年ごとの GDP を示したものです。1960 年から 2024 年までの各年が、それぞれ 1 つの列(変数)として構成されています。そのため、1 行が 1 つの国の GDP の推移を表しています。 データを眺めていると、ところどころに欠測値が存在することが分かります。 データの出典:世界銀行(https://www.worldbank.org/)取得日:2025/12/16 このデータにおいて欠測値になっている理由としては、統計の取得体制の問題や、まだ調査・集計が行われていないことなどが考えられます。この後、国ごとのGDPのトレンド把握や国同士の比較を行うのであれば、まずはデータの欠測値の状況を把握しておくことが重要です。 データ中の欠測値を調べる方法として、JMPでは「欠測値を調べる」という、欠測値のパターンを確認したり、補完を行ったりできるプラットフォーム...
 Masukawa_Nao
Masukawa_Nao

JMPの「予測プロファイル」では、「満足度の最大化」を用いることで、各応答の目的(大きい方が良い・小さい方が良い・目標値に合わせる)をできるだけ同時に満たすような因子(説明変数)の組み合わせ、いわゆる最適条件を求められます。 ただし求められた因子の最適値は、あくまで1つの点であり、実際の工程では、温度や湿度などを最適値ぴったりに制御するのは難しく、さらに環境要因などにより、因子は最適値のまわりでばらつきをもって変動すると考えるのが自然です。 因子がばらつくのであれば、それに応じて応答もばらつくことになるので、応答の値も分布を構成します。もし応答に仕様範囲(LSL:下側、USL:上側)が設定されている場合、その分布の一部が仕様限界を超え、不適合が発生する可能性があります。 下図は、因子がばらつくことを想定したときの応答(Error1)の分布の例です。ヒストグラムを見ると、仕様範囲外に位置す...
 Masukawa_Nao
Masukawa_Nao

Here are some ideas to help you get the most out of JMP Live.
 John_Powell_JMP
John_Powell_JMP
Spectral analysis is a cornerstone of analytical chemistry, materials science, and countless other fields where understanding molecular signatures drives discovery. Yet one of the most persistent challenges analysts face is baseline drift – those unwanted variations in signal intensity that can mask true spectral features and compromise quantitative analysis. Today, we're excited to showcase how J...
 lkimhui
lkimhui

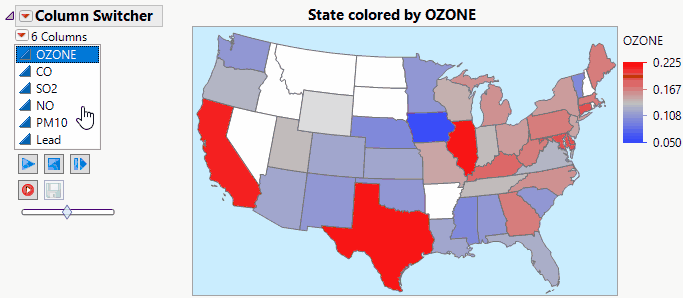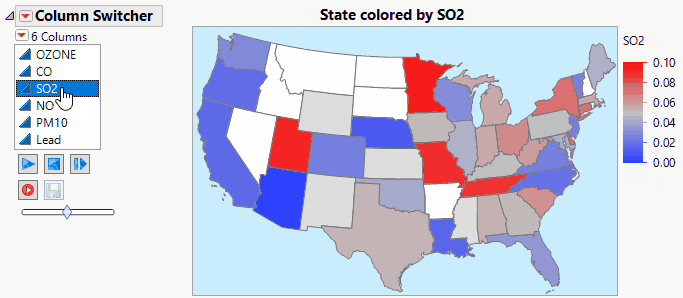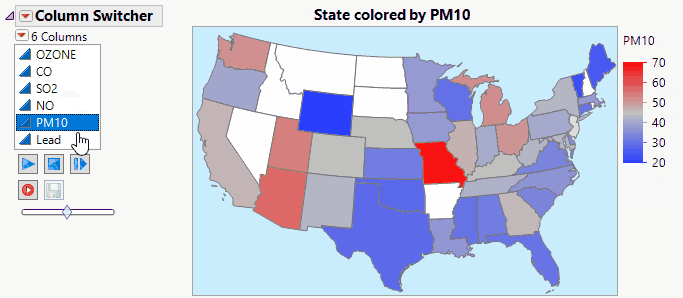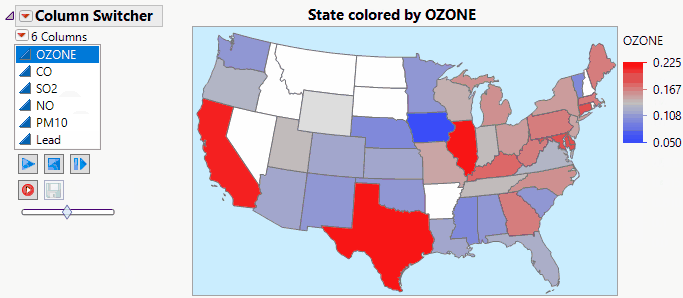
JMP Live makes Column Switchers Interactive on the Web.
 John_Powell_JMP
John_Powell_JMP
JMP offers a world-class design of experiments (DOE) platform, which has been widely used by scientists and engineers across a diverse range of industries such as the pharmaceutical, semiconductor, and chemical industries. But would you be surprised if someone told you that JMP’s DOE platform can also be of aid in your artistic endeavors? Read more to find out how!
 BillFish828
BillFish828

JMP is often targeted towards engineers and scientists that need to analyze data, but did you know that it can also be used for forecasting sales, creating production build plans, and communicating these plans with suppliers and customers? Read on to find out how.
 Jed_Campbell
Jed_Campbell

In this joint ENBIS and JMP webinar, Dr. David Meintrup compares and contrasts artificial and human intelligence and explores what we can and should reasonably expected from artificial intelligence.
 hannah_martin
hannah_martin

下のグラフのY軸に着目してください。Y軸が6つもあります! 最新版の「JMP 19」では、「グラフビルダー」において、複数のY軸を1つのグラフに表示する「複数のY軸」のオプションが追加されました。 このグラフのように、複数のY変数を1つのグラフで表現することで、次のようなメリットが得られます。 スケールの異なる変数でも、同じ時間軸でトレンド比較できる変化したタイミングを把握・比較しやすい変数間の関連性(相関)を把握しやすい ただし、これらのメリットを得られる他のグラフ作成方法も考えられます。 本記事では、工程トレンドを調べるデータに対し、JMPの「グラフビルダー」を使って、複数の工程を効果的に視覚化する方法を考えてみます。 工程データ例と共通のY軸でのグラフ化 以下は、3つの機械(Machine1~Machine3)を使って製品を製造したときの工程データです。各機械について、1秒...
 Masukawa_Nao
Masukawa_Nao

Recording and materials from this online short course, 03 December 2025. Presented by Chris Gotwalt and @Phil_Kay .
 Phil_Kay
Phil_Kay

今年の9月に、JMP製品は最新バージョンである「19」にアップデートしました。 このアップデートにより「JMP Pro」および「JMP Student Edition」には新たに「因果処置効果」というプラットフォームが追加され、傾向スコアマッチング(Propensity Score Matching)による分析を実施できるようになりました。 本記事では、この「因果処置効果」プラットフォームを用いて傾向スコアマッチングを実施する方法を、例題を用いて解説します。 傾向スコアマッチングの例題 ある医療処置の効果を調べるために、181名の患者データを収集した。各患者は「医療処置を受けた/受けていない」のいずれかに分類され、アウトカム(効果あり・なし)が判定されている。 処置やアウトカムと関連があると考えられる患者特性として、性別、年齢、喫煙歴、BMI、重症度スコアを共変量とする。 アウト...
 Masukawa_Nao
Masukawa_Nao

Introduction Welcome to the finale of our space filling DOE series! After establishing our framework and evaluation methodology in the previous posts, we now present the comprehensive results of our comparative study. The findings provide clear guidance on when and how to select the most appropriate space filling design for your specific application. Summary of key findings Our analysis across f...
 Victor_G
Victor_G
