Open Source Database (PostgreSQL, MySQL/MariaDB, or SQLite) Connection Configuration Using ODBC on a Mac
An increasing number of companies are using OpenSource Database systems to store their data. This includes PostgreSQl, MySQL/MariaDB and SQLite. While connecting to a Database using JMP's Database query can be done with a few clicks of a button; the hard work is in configuring the connection on your machine using the right driver. Things get a bit more complicated on a Mac with the lack of resourc...
 yasmine_hajar
yasmine_hajar

 Richard_Zink
Richard_Zink
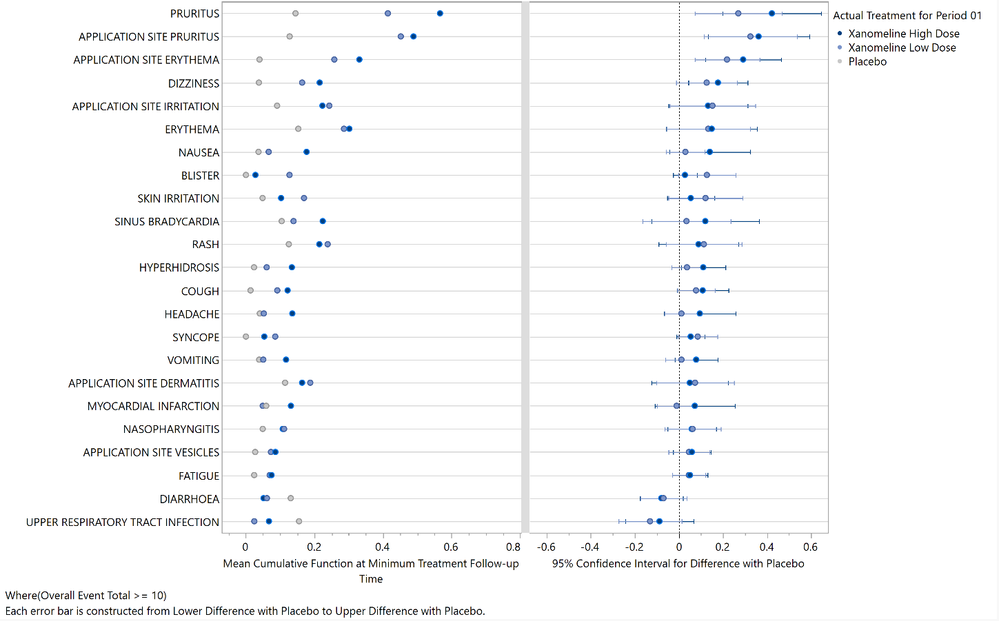
 MaddiWalsleben
MaddiWalsleben
 Masukawa_Nao
Masukawa_Nao
 anne_milley
anne_milley
 Dahlia_Watkins
Dahlia_Watkins

 Craige_Hales
Craige_Hales


 John_Powell_JMP
John_Powell_JMP
 lkimhui
lkimhui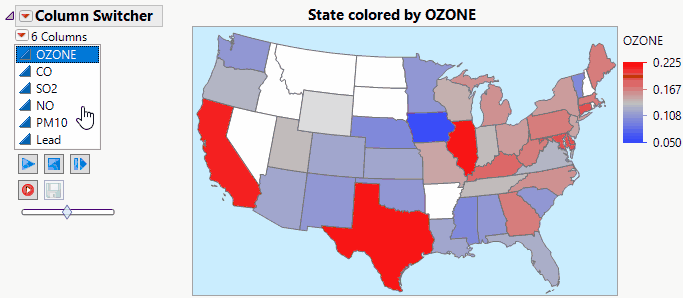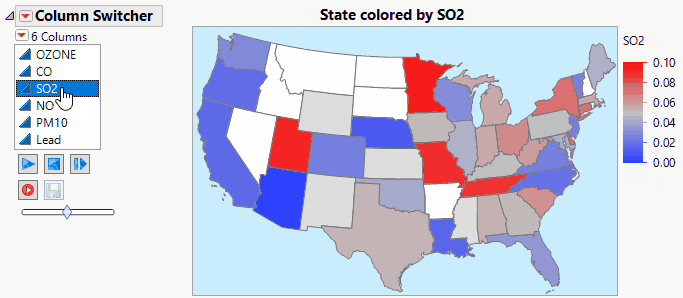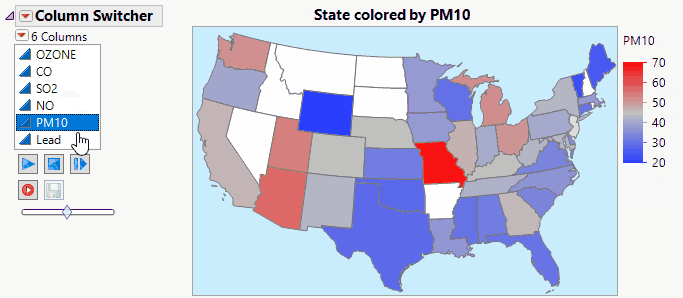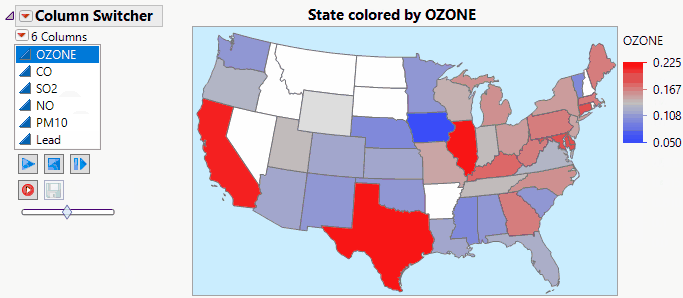

 Jed_Campbell
Jed_Campbell
 hannah_martin
hannah_martin
 Phil_Kay
Phil_Kay
