Single Sampling by Attributes
Single attributes sampling plans or MIL-STD-105E are used when the inspections can only be classified as two outcomes. One can think of this type of plan as go / no-go or in specification ...
 stan_koprowski
stan_koprowski
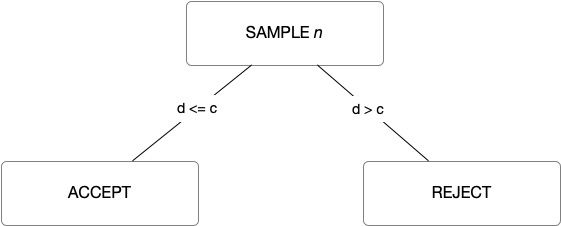
 Paul_Nelson
Paul_Nelson
 Duane_Hayes
Duane_Hayes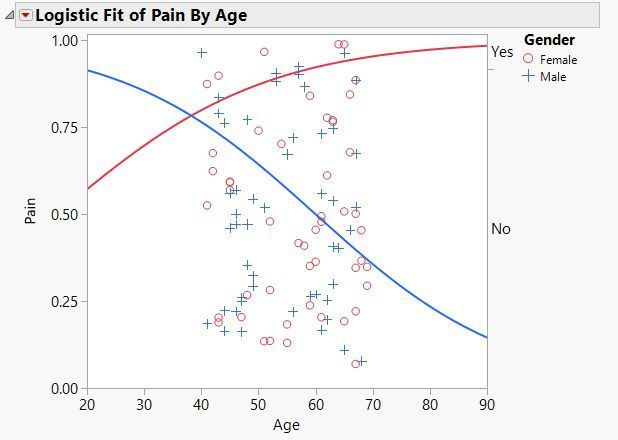
 Peter_Hersh
Peter_Hersh
 Masukawa_Nao
Masukawa_Nao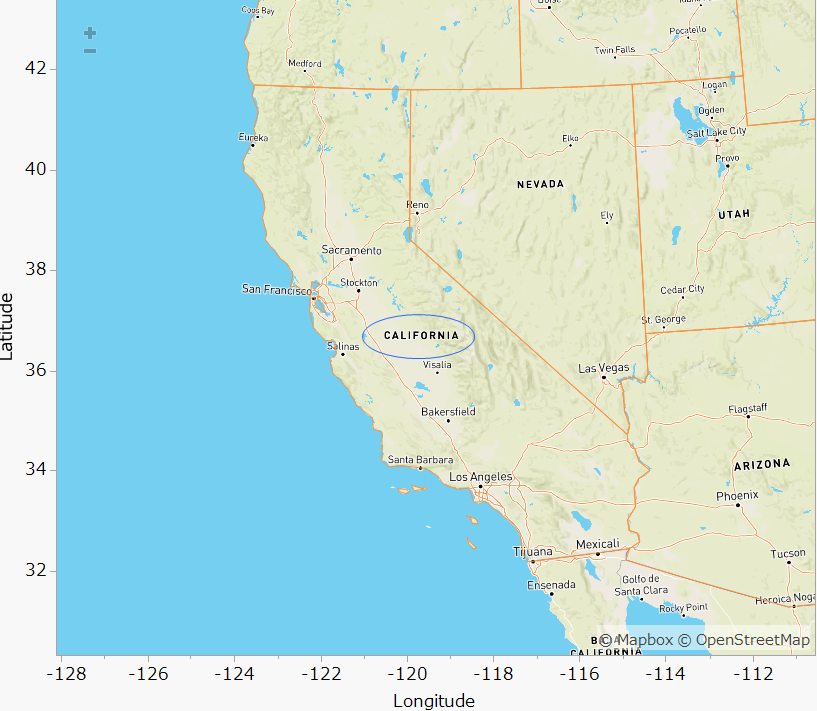
 gail_massari
gail_massari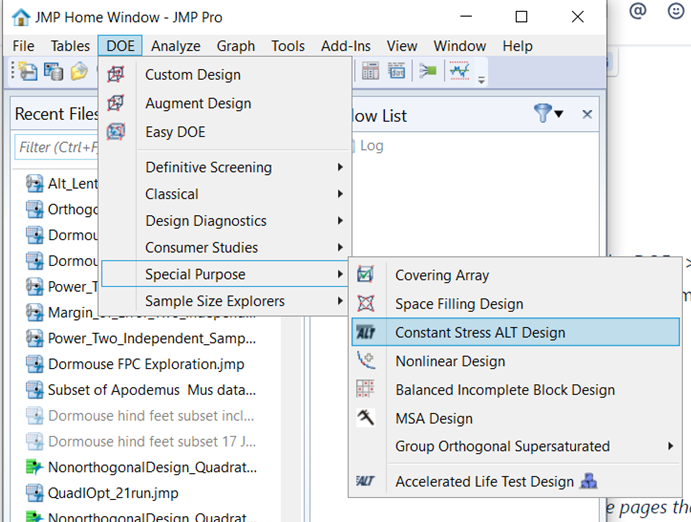

 Jed_Campbell
Jed_Campbell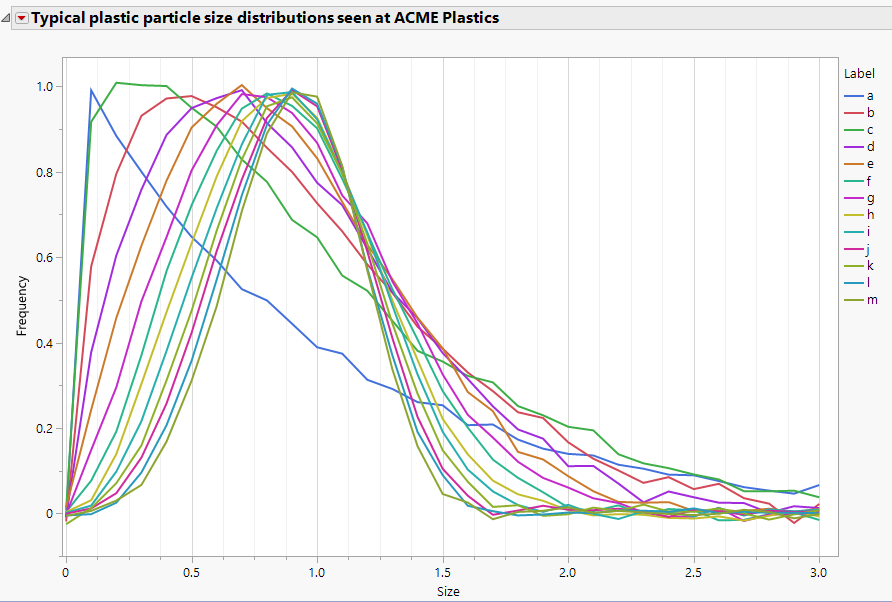
 Phil_Kay
Phil_Kay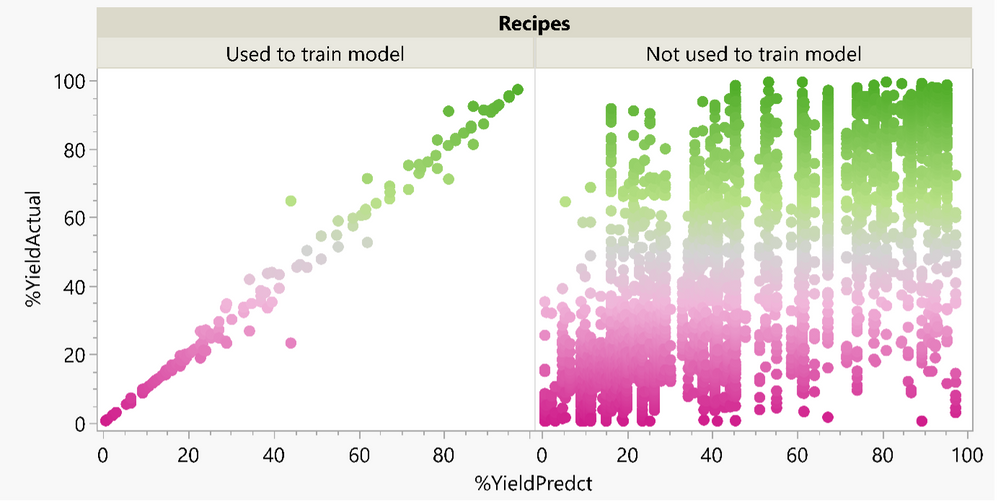
 Bill_Worley
Bill_Worley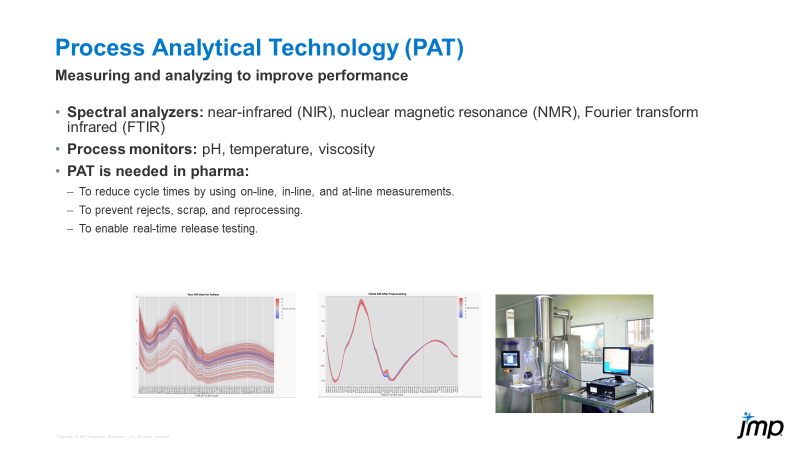
 DaeYun_Kim
DaeYun_Kim
 SamGardner
SamGardner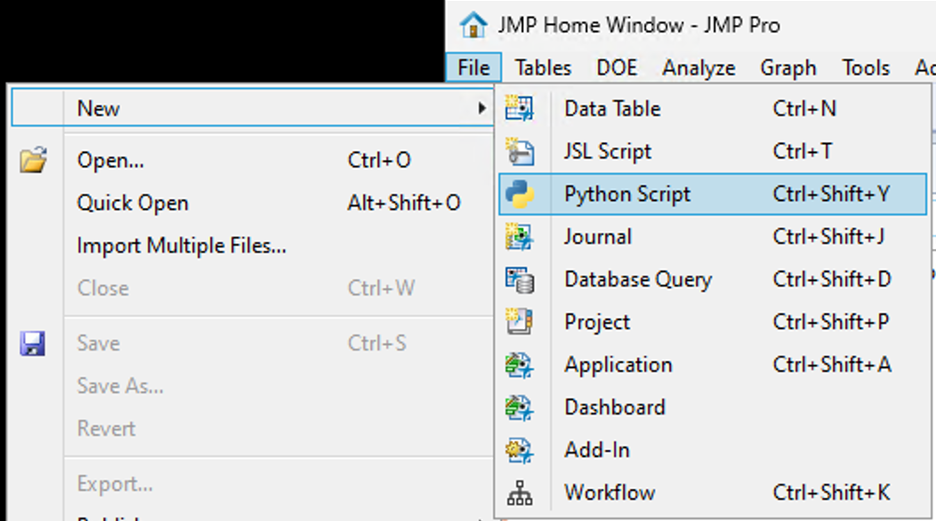

 Valerie_Nedbal
Valerie_Nedbal
 Richard_Zink
Richard_Zink KristenBradford
KristenBradford
 Chris_Kirchberg
Chris_Kirchberg
 cweisbart
cweisbart
 Craige_Hales
Craige_Hales