溶出曲線の類似性評価とは ~f2 と信頼区間を用いた溶出挙動の類似性評価 ~
医薬品開発において「溶出試験」とは、薬が体の中でどのような挙動を示すかを、試験管内で調べる試験のことを指します。 例えばジェネリック医薬品では、有効成分は同じでも、添加物や製造方法などの処方が変更されることがあります。その際、一定時間ごとに溶出率(有効成分が溶け出した割合)を測定し、変更前の製剤と変更後の製剤を比較して、溶出の傾向が類似していることを示す必要があります。 下図は、横軸を時間(分)、縦軸を溶出率とした、溶出曲線と呼ばれるものです。pH4.5、pH6.0、または水(Water)を試験液として用いた場合について、試験製剤(Test)と標準製剤(Reference)の時間ごとの溶出率をプロットし、折れ線で結んでいます。 *実際にY軸にプロットされている点は、複数のサンプル製剤の溶出率の平均値となります。 3種類の試験液における2つの曲線を比較すると、時間とともに溶出率が上昇し、1...
 Masukawa_Nao
Masukawa_Nao


 Craige_Hales
Craige_Hales


 John_Powell_JMP
John_Powell_JMP
 lkimhui
lkimhui
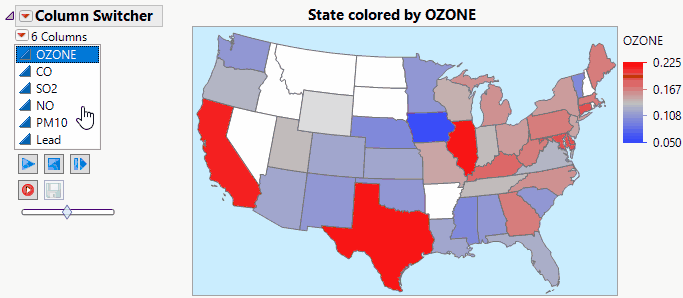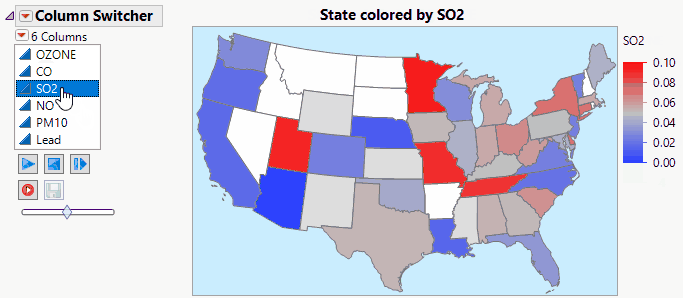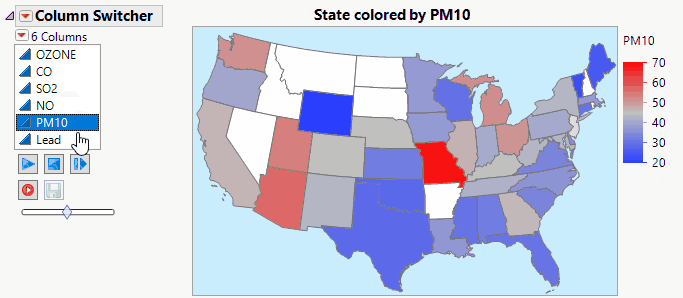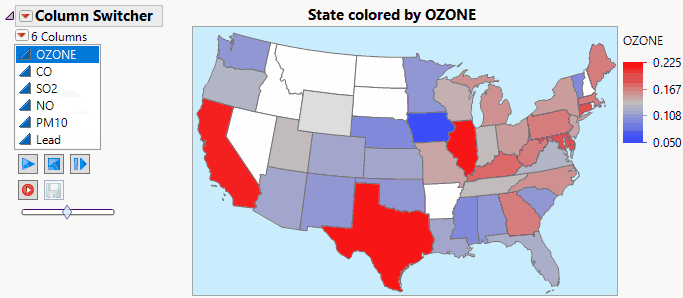

 Jed_Campbell
Jed_Campbell
 hannah_martin
hannah_martin
 Phil_Kay
Phil_Kay

 Victor_G
Victor_G

 Richard_Zink
Richard_Zink

 David_Elsheimer
David_Elsheimer
