What is simple mediation analysis?

Hamid_Sanei

What is simple mediation analysis?

When we see a strong relationship between two variables, it is natural to ask: Why does this happen? Mediation analysis helps answer that question by examining whether the effect of a predictor variable on an outcome flows, at least in part, through another variable: the mediator.

In a simple mediation model, the mediator acts as a pathway through which the predictor influences the outcome. This approach is especially useful when you want to understand the mechanism behind an observed relationship. For example, suppose we are interested in understanding the role of autonomy in mediating how feelings of school belonging affect interest in school for secondary students. By employing the simple mediation model, we can assess the significance of the indirect effect and gain insights into whether and to what extent students' autonomy mediates the impact of belonging on interest.

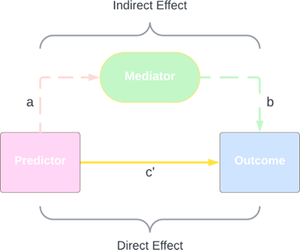
Figure 1. Conceptual diagram of a simple mediation model

As shown in Figure 1, the simple mediation model involves:

Predictor: The starting variable (sometimes called the causal variable).
Mediator: The go-between variable that transmits some of the effect.
Outcome: The end result that we want to explain.

The Predictor can affect the outcome in two ways:

Direct effect (c′ The portion of the relationship between X and Y that is not explained by the Mediator.
Indirect effect (ab The portion of the relationship that passes through the Mediator, calculated as the product of:

Path a: Predictor → Mediator
Path b: Mediator → Outcome

Total effect (c The sum of the direct and indirect effects.

Understanding the effects

Direct effect (c′): Consider two observations. Both are identical in the value of the Mediator, but one has a higher value in the Predictor. This variation in Predictor is projected to cause a c′ unit change on Outcome. If the direct effect shows a positive value, then as the Predictor increases, the Outcome will increase as well. On the other hand, if the effect is negative, a rise in the Predictor would result in a drop in the Outcome.
Indirect effect (ab The indirect effect captures the chain reaction – how much of the Predictor’s influence on the Outcome happens because it changes the Mediator, which in turn changes the Outcome. So, if you have two observations with a tiny difference in the Predictor, they could show a change of ab units in the Outcome. This happens because the Predictor first makes a splash on the Mediator, and then the Mediator ripples that effect onto the Outcome.

Path a: If you have two observations that are just one unit different on the Predictor, Path a tells us how they might differ on the Mediator. The sign (positive or negative) gives us a hint: if the Predictor goes up, the Mediator is likely to go up and vice versa.
Path b: Imagine two observations with a one-unit difference on the Mediator, but they are the same on the Predictor. This slight change in the Mediator can lead to a change of b units in the Outcome. The sign of b (positive or negative) lets us know if having more on the Mediator means we will see more or less on the Outcome.

Total effect (c = c′ + ab): Think of two observations that are almost the same, but with a one-unit difference in the Predictor. In mediation analysis, this slight change can affect the Outcome. The total effect helps us figure out how much this slight change in the Predictor might change the Outcome. It is like gauging the impact of a slight change by measuring the predicted difference in the Outcome between two observations that have a one-unit variation on the Predictor.

Example: Belonging, autonomy, and interest in school

Now that we have covered the basic idea, let us see how a simple mediation analysis works in practice. For this example, we will explore data from secondary students from diverse backgrounds across the United States, focusing on three key variables:

Belonging: Perception of belongingness within school, including feelings of connection and inclusion (Predictor).
Autonomy: The degree to which an individual feels a sense of independence and control over their academic choices, decisions, and actions (Mediator).
Interest: Measure of enthusiasm and engagement in school subjects (Outcome).

Our research question: Does Autonomy help explain the link between school Belonging and Interest? In other words, is the effect of Belonging on Interest partly transmitted through Autonomy?

We begin by opening the Secondary Students.jmp data table, which you can find in JMP’s Sample Data folder. With the data open, go to Analyze > Multivariate Methods > Structural Equation Models. In the launch window, select Interest, Belonging, and Autonomy as the model variables, then click OK to open the platform. From there, click the Model Shortcuts red triangle and choose Cross-Sectional Classics > Mediation Analysis. In the Specify Mediation Model window, set Belonging as the Causal Variable, Autonomy as the Mediator Variable, and Interest as the Outcome Variable. Finally, click Run to fit the simple mediation model. To get standardized estimates, right-click anywhere on the Path Diagram and select Show > Show Estimates > Standardized. Similarly, you can select Show and select or deselect suggested indices, such as R-squared values.

Figure 2. Mediation analysis model report

Understanding the output

Right away (see Figure 2), the Parameter Estimates table tells us about the direct effects:

Path a (Belonging → Autonomy): 0.298, meaning that for two students who differ by one unit on Belonging, they are estimated to differ by 0.298 units on Autonomy.
Path b (Autonomy → Interest, controlling for Belonging): 0.337, meaning that for two students equal on Belonging scores but differing by one unit in their Autonomy scores, they are estimated to differ by 0.337 units on Interest.
Path c′ (Belonging → Interest, controlling for Autonomy): 0.624, meaning that for two students who differ by one unit on Belonging but are equal on Autonomy, they are estimated to differ by 0.624 units on Interest.

These results suggest that students with higher Belonging tend to have higher Autonomy (positive Path a), and that higher Autonomy is associated with greater Interest in school (positive Path b).

From direct to total effects

To see the total effect (c) and indirect effect (ab), click the Mediation Analysis red triangle and select Total Effects and Indirect Effects.

Figure 3. Total and indirect effects estimates

Here is what Figure 3 indicates:

Indirect effects (ab) = 0.298 × 0.337 = 0.100, meaning that for two students that differ by one unit in their Belonging, they are estimated to differ by 0.100 units on Interest as a result of the tendency for those with higher Belonging to have higher Autonomy (positive Path a), which translates into greater Interest (positive Path b). This significant effect suggests that changes in Belonging have an impact on Interest, while part of this influence is channeled through changes in the mediator Autonomy.
Total effects (c) = 0.624 + 0.100 = 0.724, meaning that every one-unit increase in Belonging is associated with an estimated 0.724-unit increase in Interest, while controlling for the Autonomy variable. Part of this effect is explained by Autonomy (0.100), meaning that Autonomy plays a small but significant mediating role in the Belonging-Interest relationship. Unsurprisingly, the total effect is a greater value compared to the direct effect (c′ = 0.624), because both Paths a and b were positive and, therefore, their product will be a positive value. As a result, the total effect, c = c′ + ab, will be greater than the direct effect (c′). This outcome happened because:

Higher Belonging results in higher Autonomy (positive Path a).
Higher Autonomy means higher Interest when controlling for Belonging (positive Path b).

Adding statistical confidence

To get more robust evidence, we can use bootstrapping to estimate confidence intervals for the indirect effect. This approach provides more accurate standard errors and confidence intervals for the indirect effect. Right-click the Estimate column in the Indirect Effects table, select Bootstrap:

Enter Number of Samples: 500
Enter Random Seed: 1234
Click OK.

Figure 4. Bootstrap distributions and confidence limits

As Figure 4 indicates, the mean for bootstrap estimates is 0.101, which is almost the same as the estimated indirect effects shown in Figure 3. The resulting Bootstrap Confidence Limits show that the indirect effect confidence interval does not include zero, confirming it is statistically significant.

Conclusion

By walking through this example, we have demonstrated how mediation analysis in JMP Pro makes it easy to separate direct and indirect effects, quantify mediation, and test its statistical significance – all without leaving the SEM platform. Mediation analysis is like being a detective; it is all about figuring out the "how" and "why." Mediation analysis helped explain why feeling a sense of belonging in school makes students more interested in their studies: Does belonging directly make students keen on school? Or does it perhaps work in a roundabout way? In mediation terms, we referred to these as direct and indirect effects. So, we got a glimpse into the behind-the-scenes action – how exactly does this feeling of belonging boost a student's enthusiasm for learning? It is all about uncovering that hidden mechanism that links belonging to interest.

Additional resources

Hayes, A. F. (2017). Introduction to mediation, moderation, and conditional process analysis: A regression-based approach. Guilford Publications.