To data connector or to not data connector, that is the question.
Is a data connector always necessary? Data connectors are an exciting addition to JMP, but they are not always necessary in every instance. This article discusses each data connector type within the new data connector framework to help you determine the best method for accessing your data.
 Dahlia_Watkins
Dahlia_Watkins

 Masukawa_Nao
Masukawa_Nao

 Craige_Hales
Craige_Hales


 John_Powell_JMP
John_Powell_JMP
 lkimhui
lkimhui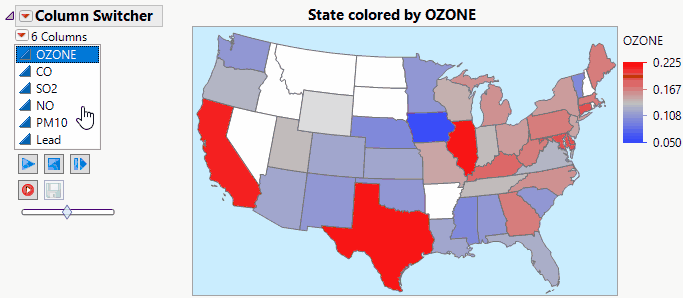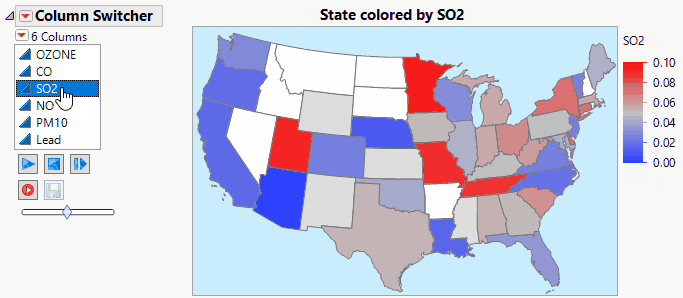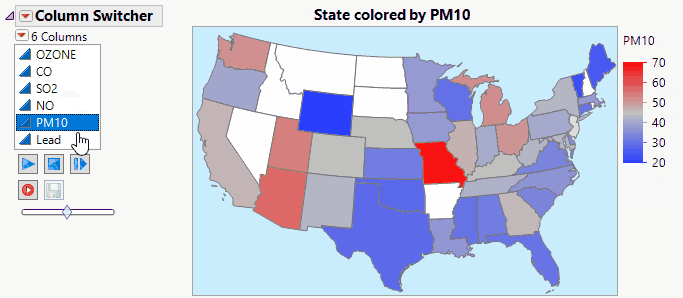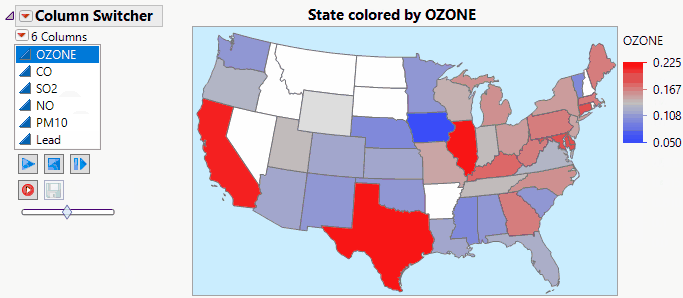

 Jed_Campbell
Jed_Campbell
 hannah_martin
hannah_martin
 Phil_Kay
Phil_Kay

 Victor_G
Victor_G

 Richard_Zink
Richard_Zink

 David_Elsheimer
David_Elsheimer