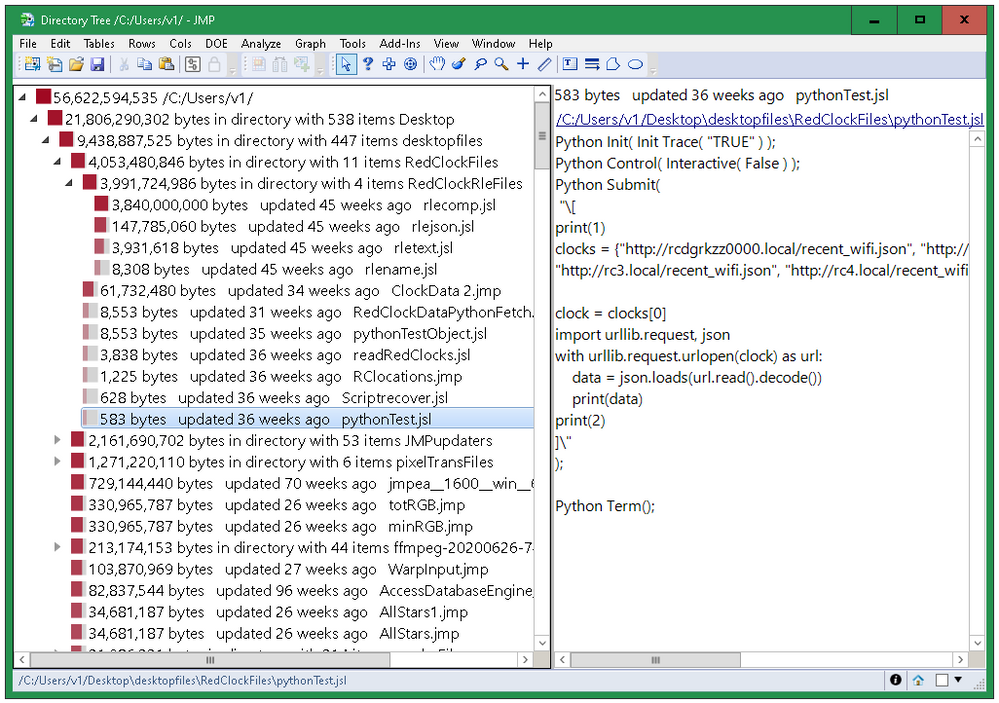
Directory Tree: Explore Space Used by Folders
See which folders are using the most space.
 Craige_Hales
Craige_Hales
See which folders are using the most space.
 Craige_Hales
Craige_Hales
Do you use JMP and Python? Are you using them independently? Python for certain things…JMP for others? Did you know that there are many ways they work...
 wendytseng
wendytseng


A group of JMP System Engineers demonstrate how easily JMP and Python can be integrated to handle everyday tasks like cleaning data, and more advanced...
 Bill_Worley
Bill_Worley

先日、日本のお客様向けに「JMPを用いた統計的仮説検定入門」という題目でWebセミナーを実施しました。セミナーの特性上、医療や医薬関係に従事している方が多く参加すると思っていたのですが、実際は半導体、電気・電子部品、素材などを開発している製造業の方々も多く参加されました。 このセミナーでは、JM...
 Masukawa_Nao
Masukawa_Nao

Is your data obscuring your data labels?
 Byron_JMP
Byron_JMP

If you've wondered how to import your database using JMP's embedded Python environment, here are some examples that may help you get started. In the f...
 Dahlia_Watkins
Dahlia_Watkins

Use JSL to control a web browser.
 Craige_Hales
Craige_Hales
In our first of a series relevant to anyone creating or testing software applications, we begin with "What is Software Testing?"
 Ryan_Lekivetz
Ryan_Lekivetz

JMPでは、[グラフ] メニューに「三角図」というグラフを作成できるプラットフォームがあります。3つの成分をもつデータをグラフ化し、分布やばらつきを調べるのに有用なグラフではありますが、実験計画法における配合実験で用いると効果的なケースがあります。 「三角図」では、以下に示したようなグラフを描く...
 Masukawa_Nao
Masukawa_Nao

先週末、世界中がパリオリンピックの選手の活躍に注目していた中、アメリカでは7月の雇用統計が発表されました。今回の雇用統計では失業率が市場予想を上回り、景気後退のシグナルである「サームルール(Sahm Rule)」が点灯されたことが話題となりました。 サームルールとは、元FRBのクローディア・サー...
 Masukawa_Nao
Masukawa_Nao

Bland-Altman分析は、2つの測定方法の一致性を評価するための統計的手法であり、主に医療や製造の分野で広く用いられています。以下に示すのは、Bland-Altaman分析を行う際に使用される「Bland-Altmanプロット」というグラフです。このプロットでは、縦軸に2つの測定値の差を、横軸...
 Masukawa_Nao
Masukawa_Nao


Maria Lanzerath, W.L. Gore's global statistics leader, advocates statistics, the scientific approach.
 anne_milley
anne_milley

This article demonstrates two ways to overlay histograms (and distribution curves) using Distribution and Graph Builder.
 sseligman
sseligman

どちらのグラフが好きですか? JMPユーザに、以下のような2のグラフ(A,B)を提示し、好ましい方を選んでいただきます。その後、別のパターンのグラフを提示し、同様に好ましいグラフを選んでいただきます。 これは、複数の選択肢から最も好ましいものを選ぶ「選択実験」を行っている状況です。選択実験を通...
 Masukawa_Nao
Masukawa_Nao

Here are my favorite helps for JSL.
 MikeD_Anderson
MikeD_Anderson

 DaeYun_Kim
DaeYun_Kim

We are thrilled to invite you to take part in the pilot of the JMP Wish List Prioritization Survey, set to launch on July 3! Your feedback is invaluab...
 LandraRobertson
LandraRobertson

熱戦が繰り広げられていたパリオリンピックが閉会しました。猛暑が続いたため、屋外には出ずに屋内でオリンピック観戦を楽しんでいた方も多かったことでしょう。 2週間程度のオリンピックでしたが、日本は合計45個のメダルを獲得し、海外大会のオリンピックでは最多の獲得数となりました。とはいっても、前回の東京...
 Masukawa_Nao
Masukawa_Nao
