どちらのグラフが好きですか? JMPユーザに、以下のような2のグラフ(A,B)を提示し、好ましい方を選んでいただきます。その後、別のパターンのグラフを提示し、同様に好ましいグラフを選んでいただきます。

これは、複数の選択肢から最も好ましいものを選ぶ「選択実験」を行っている状況です。選択実験を通じて、どのスタイルのグラフが最も好ましいのかを調べることができます。
実は昨年、この選択実験を日本のお客様に実施し、その結果を分析するセミナーを開催しました。本ブログでは、その際に行った選択実験の内容と結果の概要をご紹介します。
JMPのグラフスタイルに関する調査
調査の目的は、JMPで出力されるグラフに関する以下の4つ(①~④)のスタイルについて、最も好ましい設定の組み合わせを見つけることです。

| スタイル |
選択肢 |
| ①グラフの境界線 |
あり、なし |
| ②目盛りの位置 |
外側、内側 |
| ➂ウィンドウの背景色 |
白、薄い灰色、濃い灰色 |
| ④フレームの境界線 |
あり、なし |
表の赤字で示した選択肢は、JMPのデフォルト設定です。この設定が本当に最適なのでしょうか?
選択モデルとは
この疑問を調べるために選択実験を行い、得られたデータを分析するモデルを「選択モデル」と言います。これは「選択型コンジョイント分析」とも呼ばれます。
選択実験によりデータを条件付きロジスティック回帰によりモデル化し、ある設定が好まれる確率を推定します。

JMPでは、「選択モデル計画」プラットフォームで選択実験の計画表を作成し、計画表に調査結果を入力、選択モデルのあてはめを行う手順で分析を実施します。
分析の手順と結果
選択実験計画の作成
[選択モデル計画] では、最初に属性(今回の例ではグラフのスタイル)の名前とその属性水準(選択肢)を設定します。

最後に設定する「計画の生成」では、以下のA, Bの設定が重要です。

A. 1選択肢あたりのプロファイルの個数: 一度に比較するグラフの個数を指定します。ここでは"2"と設定しているので、2つのグラフを提示し、どちらが好ましいかを選択してもらうことになります。
B. 1アンケートあたりの選択肢集合の個数:設問数です。ここでは"8"と設定しているので、どちらが好みかという2者択一の質問を8パターン回答していただくことになります。
計画テーブルに基づいて調査を実施し、調査結果(応答)を入力
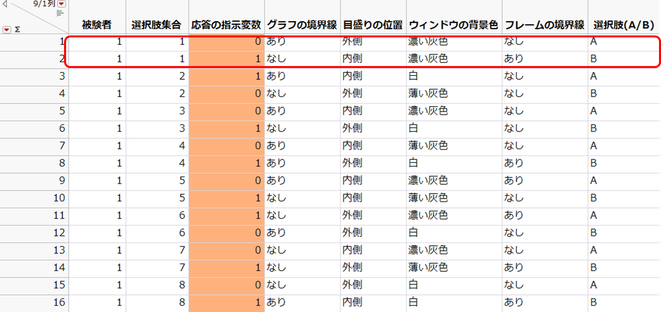
作成された計画テーブルに基づいて調査を行い、その結果をデータテーブルに入力します。下記のテーブルは、ある1名の回答者に対する結果です。8つの選択肢集合があり、各選択肢集合には2つの回答選択肢(A,B)があるので16行で構成されています。
列「応答の指示変数」(オレンジ色で塗られた列)には、選ばれた選択肢に"1"、選ばれなかった選択肢に"0"を入力します。例えば下図の赤枠の箇所は、最初の選択肢(A,B)でBが好ましいと回答したので、列「応答の指示変数」の箇所は1行目が"0"、2行目が"1"と入力しています。
この作業を回答者の数だけ行います。今回の調査では97名の方に回答いただいたので、97名分のデータを作成しました。参考までに、各選択肢のグラフ(8パターン)とその回答の分布を、本ブログの資料(Choice_Results.pdf)として添付しています。
選択モデルのあてはめ
データテーブルに含まれているスクリプト「選択モデル」をクリックし、選択モデルをあてはめます。得られたレポートは以下の通りです。

選択モデルのようなコンジョイント分析では「効用」という用語が登場しますが、ここでは「グラフに関する満足度」と捉えてください。
レポート「パラメータ推定値」では、各項目が効用に対してどのぐらい影響しているのか(部分効用という)を示す係数の推定値、標準誤差が示されています。
レポート「尤度比検定」では各要因の有意差検定の結果が表示されています。この例で有意水準5%で有意なのは、「グラフの境界線」と「フレームの境界線」の2つです。すなわちグラフの境界線があるかないか、またはフレームの境界線があるかないかの違いが効用に影響を及ぼしていると考えられます。
効用プロファイル
各因子(スタイル)の水準(選択肢)に対する効用の予測値をグラフ化したものが、以下の「効用プロファイル」です。このグラフにより、選択肢を変更すると効用がどのように変化するかを確認できます。効用の予測値は、前述のパラメータ推定値(部分効用)から求められます。
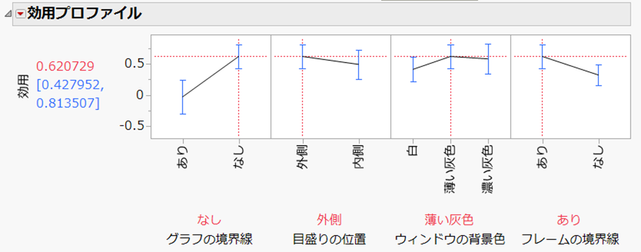
効用を最大化(すなわちグラフの満足度を最大化する)設定は、以下の設定になります。
グラフの境界線:なし
目盛りの位置:外側
ウィンドウの背景色:薄い灰色
フレームの境界線:あり
これは、何とJMPのデフォルト設定です! 97名の回答から、結局のところJMPのデフォルト設定が最も良いスタイルだということが分かりました。
では、JMPのデフォルト設定に対して、フレームの境界線がない設定を比較したとき、それぞれのグラフが選択される確率を求めてみましょう。
このことを、オプションである [確率プロファイル] を選択して確認することができます。下側の「基準」にJMPのデフォルト設定を指定し、プロファイル部分に比較したい設定の水準を指定します。

このときの確率(縦軸)は、0.376と表示されています。これにより、次のようにそれぞれの選択確率が求められます。
JMPのデフォルト設定が選択される確率:0.624 (1 - 0.376)
比較したい設定が選択される確率:0.376
ここでは示しませんが、[多選択プロファイル] のオプションを用いると、3つ以上のスタイルの設定について選択確率を求めることができます。
とりあえず、JMPのデフォルト設定が最適なグラフ設定だという結論が得られて安心しました。
by 増川 直裕(JMP Japan)
Naohiro Masukawa - JMP User Community
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.