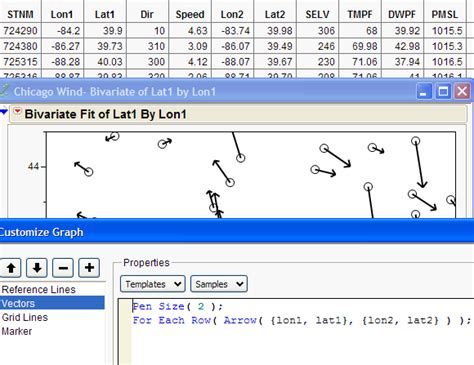
Level Up your Python game with JMP: Cleaning data with Python and JMP
A group of JMP System Engineers demonstrate how easily JMP and Python can be integrated to handle everyday tasks like cleaning data, and more advanced...
 Bill_Worley
Bill_Worley

 Masukawa_Nao
Masukawa_Nao
 Byron_JMP
Byron_JMP
 Dahlia_Watkins
Dahlia_Watkins
 Craige_Hales
Craige_Hales
 Ryan_Lekivetz
Ryan_Lekivetz



 anne_milley
anne_milley

 sseligman
sseligman

 MikeD_Anderson
MikeD_Anderson
 DaeYun_Kim
DaeYun_Kim
 LandraRobertson
LandraRobertson
 MaddiWalsleben
MaddiWalsleben
 XanGregg
XanGregg