Level up your Python game with JMP
Do you use JMP and Python? Are you using them independently? Python for certain things…JMP for others? Did you know that there are many ways they work...
 wendytseng
wendytseng
Do you use JMP and Python? Are you using them independently? Python for certain things…JMP for others? Did you know that there are many ways they work...
 wendytseng
wendytseng

A group of JMP System Engineers demonstrate how easily JMP and Python can be integrated to handle everyday tasks like cleaning data, and more advanced...
 Bill_Worley
Bill_Worley

If you've wondered how to import your database using JMP's embedded Python environment, here are some examples that may help you get started. In the f...
 Dahlia_Watkins
Dahlia_Watkins

This article demonstrates two ways to overlay histograms (and distribution curves) using Distribution and Graph Builder.
 sseligman
sseligman

Here are my favorite helps for JSL.
 MikeD_Anderson
MikeD_Anderson

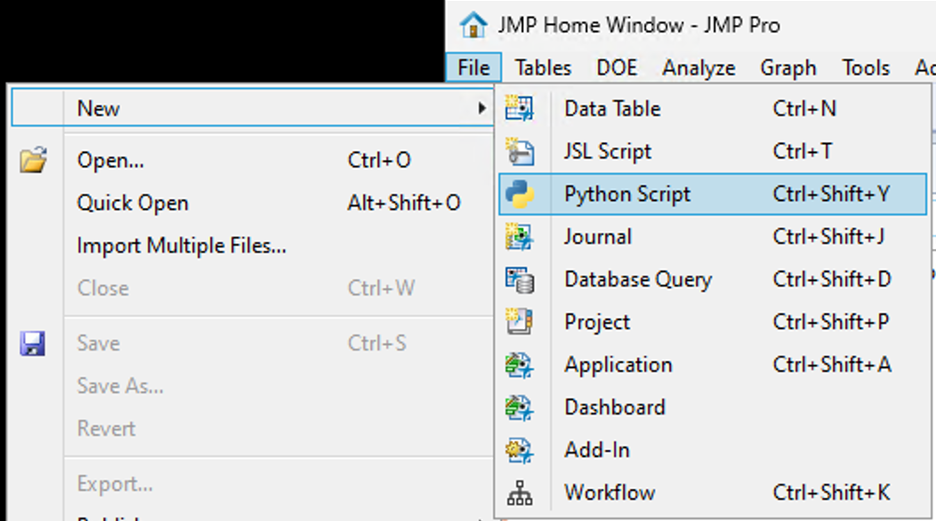
Get familiar with the Python integrated development environment (IDE) in JMP 18 and learn how to: Locate the Python IDE.Run a simple example.Install P...
 yasmine_hajar
yasmine_hajar

You want to keep coding in JSL, but for a particular function, you know there's an easy way to write it in Python. So how do you create a JSL function...
 Paul_Nelson
Paul_Nelson

Introduction A genome-wide association study (GWAS) is an approach that involves rapidly scanning genetic markers (or SNP or Single Nucleotide Polymor...
 Valerie_Nedbal
Valerie_Nedbal

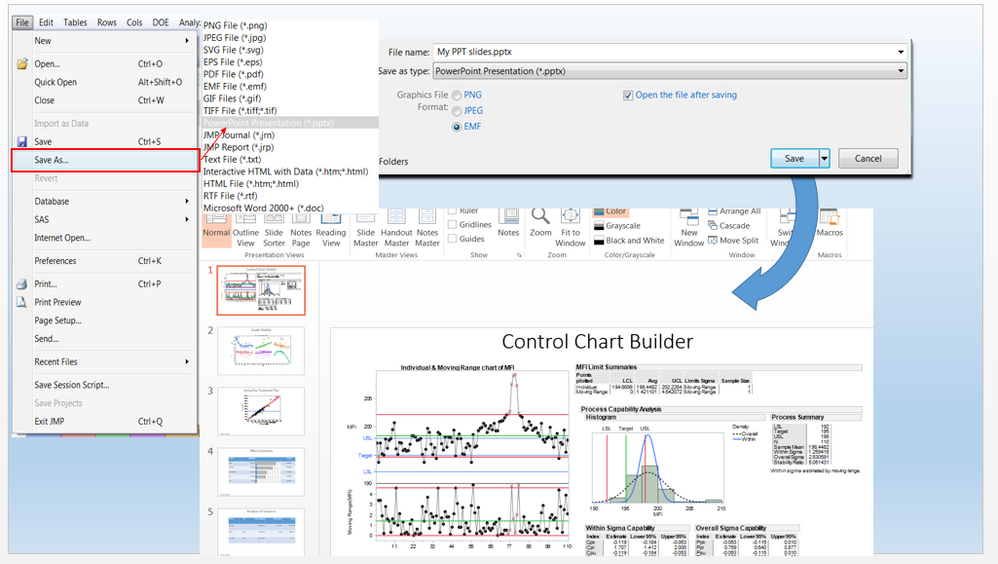
Here's how you can export JMP reports directly into the .pptx file format.
 MaryLoveless
MaryLoveless
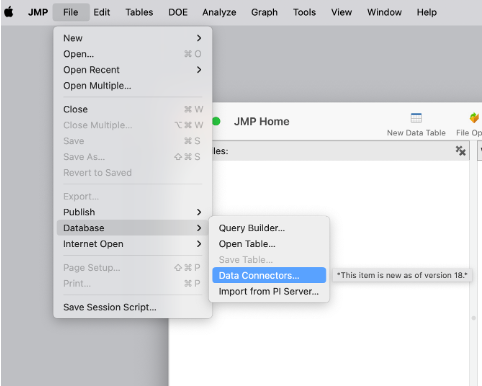
JMP 18 has a new way to integrate with Python. The JMP 18 installation comes with an independent Python environment designed to be used with JMP. In a...
 SamGardner
SamGardner
Often as we are trying to gain insights from our data, understanding that two variables are related is not enough. We need to dig deeper and ask quest...
 haleyyaremych
haleyyaremych

Is it important to spot subtle, elusive shifts in your process?
 AnnieDudley
AnnieDudley

Population studies are a fascinating subfield of genetics that focus on understanding genetic differences within and among populations to reveal a pop...
 Valerie_Nedbal
Valerie_Nedbal

There are quite a few great new capabilities in JMP Pro 18: updates to GLMM; more genomics capabilities; mixed models and response screening for big d...

This month, I begin the first of a three-part process to attempt to demonstrate how to apply the SEM concepts that I have introduced in previous JMPer...
 jordanwalters
jordanwalters

Data access is fundamental. It’s often the first step in the analytic workflow, but it's frequently a source of frustration for scientists and enginee...
 Daniel_Valente
Daniel_Valente

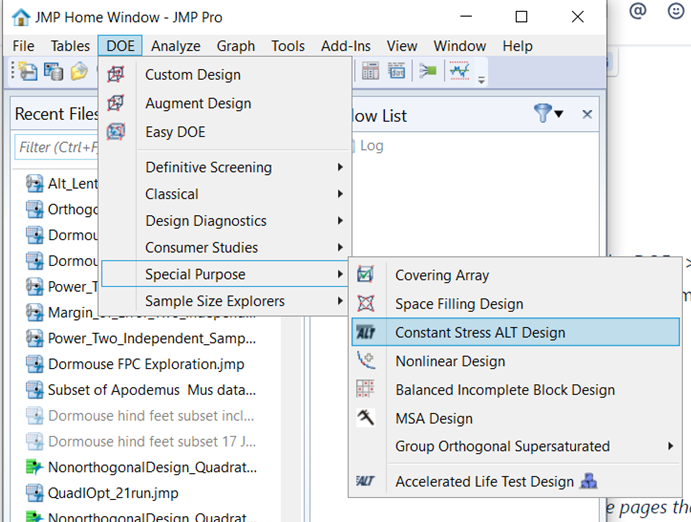
How do you decide what designer to use from the DOE menu in JMP?
 bradleyjones
bradleyjones

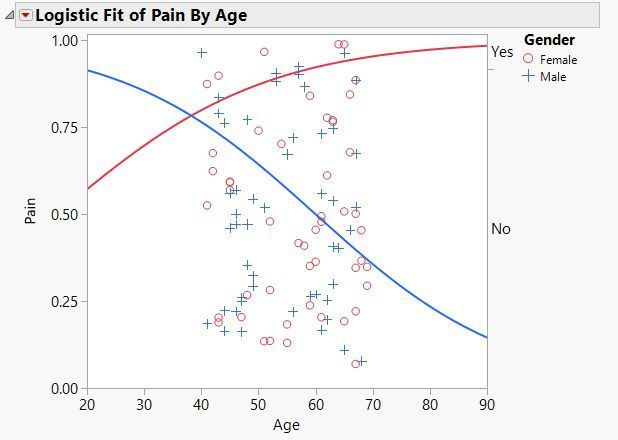
Odds ratios are difficult to interpret in the presence of interaction terms and higher order terms. This post will show you how to produce odds ratios...
 Duane_Hayes
Duane_Hayes
New JMP 18 Constant Stress Accelerated Life Test (CSALT) uses experiment design principles to determine the number of units to test at a variety of s...
 gail_massari
gail_massari