JMP Live tips and tricks
Here are some ideas to help you get the most out of JMP Live.
 John_Powell_JMP
John_Powell_JMP
Here are some ideas to help you get the most out of JMP Live.
 John_Powell_JMP
John_Powell_JMP
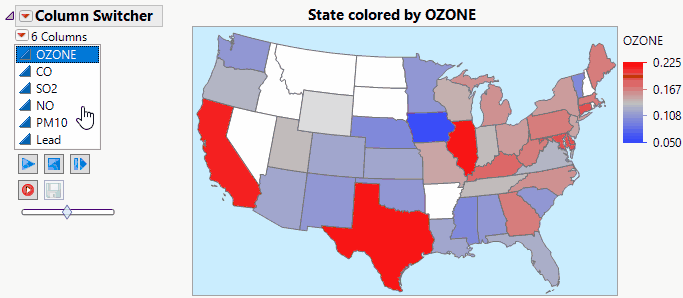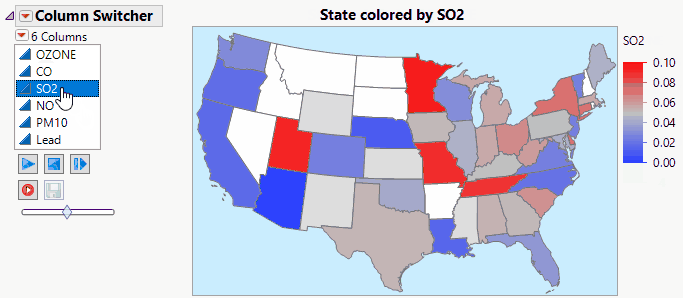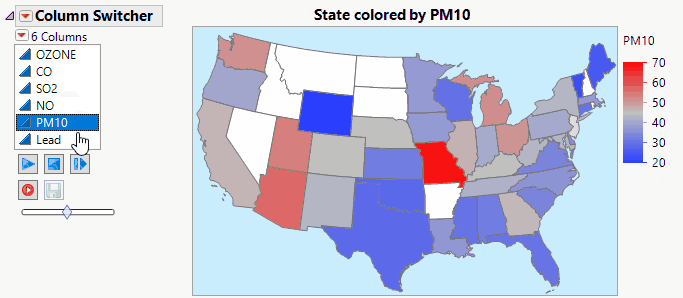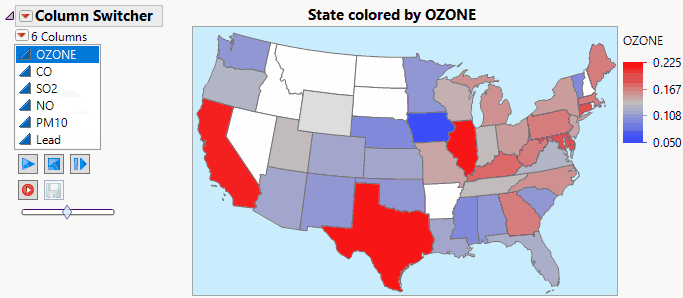
JMP Live makes Column Switchers Interactive on the Web.
 John_Powell_JMP
John_Powell_JMP
We explore an extension to the classic Pareto plot.
 Richard_Zink
Richard_Zink

The Custom Floorplan Heatmaps extension enables users to visualize environmental monitoring data at each time point for an entire floorplan.
 David_Elsheimer
David_Elsheimer

The Survival Explorer add-in produces a dynamically updating Kaplan-Meier plot with an accompanying number at risk table.
 Richard_Zink
Richard_Zink

There are four common time-based values that you might have to deal with in JMP: dates, times, datetimes and durations.
 Jeff_Perkinson
Jeff_Perkinson

The latest release of JMP Clinical makes it the most sophisticated visualization and analysis tool for clinical trials the market. It has as much to do with our teams that build the software as it does its amazing functionality. Building on the powerful functionality of JMP Pro, JMP has delivered a solution that addresses the needs of a wide audience, including safety surveillance teams, medical m...
 geoffrey_mann
geoffrey_mann

When two variables are related, the natural next question is “why?” Mediation analysis helps answer that by testing whether a third variable, the mediator, explains how the predictor influences the outcome. It moves us from “X is related to Y” to “X affects Y by changing M.” For example, in education research, we might find that students who feel a strong sense of belonging are more interested in ...
 Hamid_Sanei
Hamid_Sanei

JMP Marketplace is an online platform to help you extend JMP as your needs evolve. Like other app stores, JMP Marketplace offers a curated selection of fully tested applications, add-ins, data connectors, and other extensions that enhance and expand JMP’s powerful capabilities. Watch a demo of the Marketplace here.
 kristen-slappey
kristen-slappey

When treatment is binary, the Causal Treatment personality in JMP enables you to choose between four estimation techniques: inverse probability weighting with ratio adjustment (IPWR), regression adjustment (REGADJ), augmented inverse probability weighting (AIPW), and propensity score matching. You may be comfortable with one of these estimation methods, or you may have no idea where to begin. Alon...
 MeichenDong
MeichenDong

Randomized controlled trials (RCTs) and other carefully designed statistical experiments are the gold standard for answering questions about cause and effect. Randomly assigning experimental units (for example, participants in a clinical trial) to treatment and control groups balances the two groups so as to minimize the chance of substantive differences between them other than those caused by any...
 MeichenDong
MeichenDong

Data access is fundamental to JMP. For the last several releases, we've been building infrastructure so that you can access data efficiently, regardless of where it lives. Once you to get the data you need into JMP, you can begin answering the questions you have. Every version of JMP adds new efficiency gains, performance improvements, and workflow additions. JMP 19 continues that trend.
Prefer vi...
 willmorgan
willmorgan

JMP 19 brings many improvements for Graph Builder. Here are a few of the most significant additions. Constrained smoothers The smoother element has a new method called P-Spline. It’s a cubic spline, just like the existing Spline method, but it’s parameterized in a way that better supports constraints. Monotonic trend curves are the most requested smoother feature, and now it’s possible – and then ...
 XanGregg
XanGregg

JMP’s latest release brings a fresh wave of updates to the Design of Experiments (DOE) platform, with new tools and smarter workflows that make it easier to design, simulate, and explore experiments. Whether you're screening factors, simulating responses, planning sample sizes, or trying to pinpoint the root cause of a failure, there’s something new to try out. Smarter fault localization with Baye...
 Ryan_Lekivetz
Ryan_Lekivetz

Data tables come in many sizes. Occasionally, I work with a table that is small enough to fit on screen: no scrolling necessary and everything I need, I can see. Most of the time, however, my data tables are tall, wide, complex, and multifaceted. For tables like these, the new data table organization and filtering tools in JMP shine. Let’s explore some real data to see why. I’ve been a longtime fa...
 julian
julian
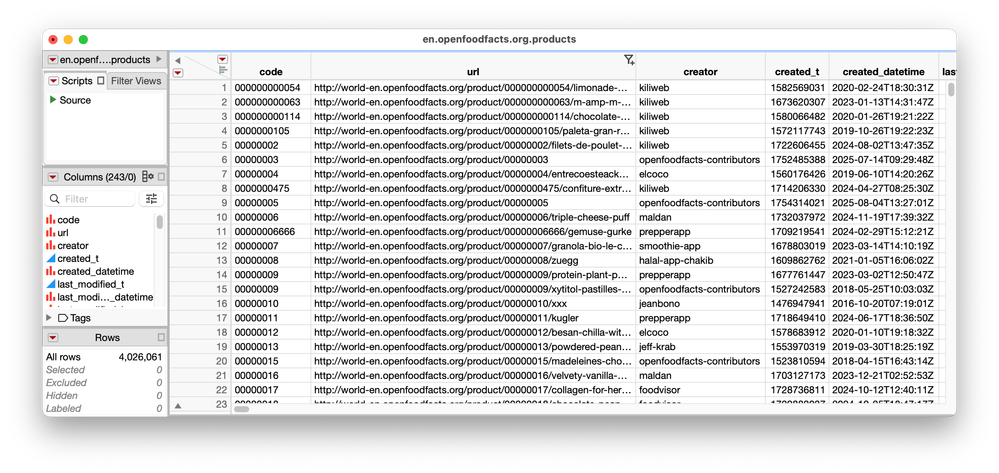
JMP’s latest release builds on the Python integration support that was introduced in JMP 18 by focusing on a fundamental part of the workflow: data access. By expanding data table operations and Python-JSL interoperability, accessing data becomes simple and convenient. Prefer video? Watch it here. Data Table operations The jmp.from_dataframe() function provides an efficient way to convert exte...
 Evan_Carr
Evan_Carr

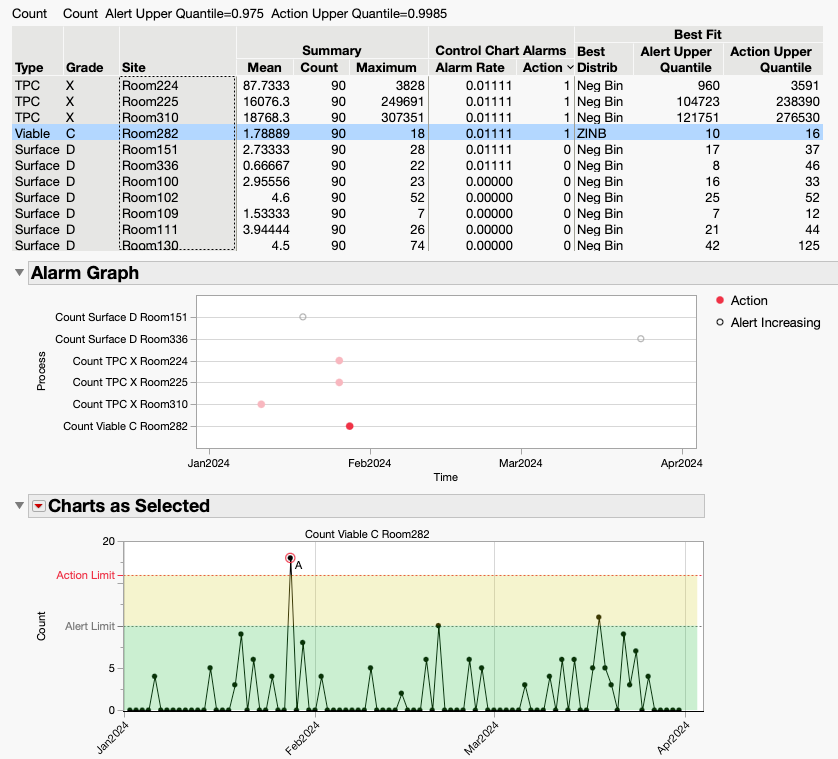
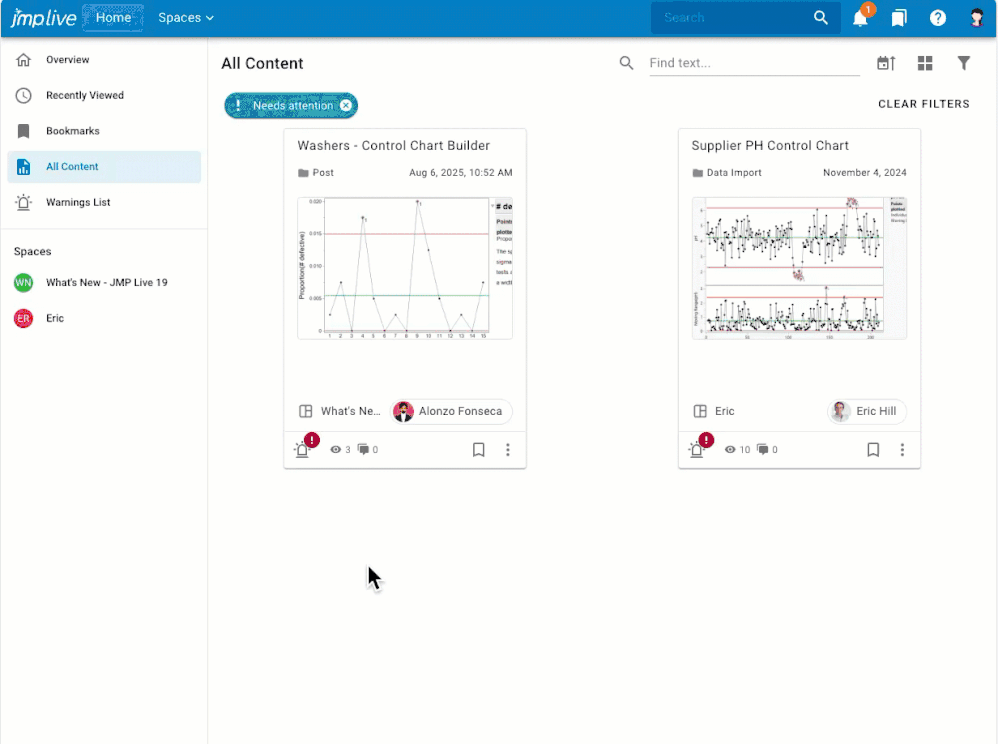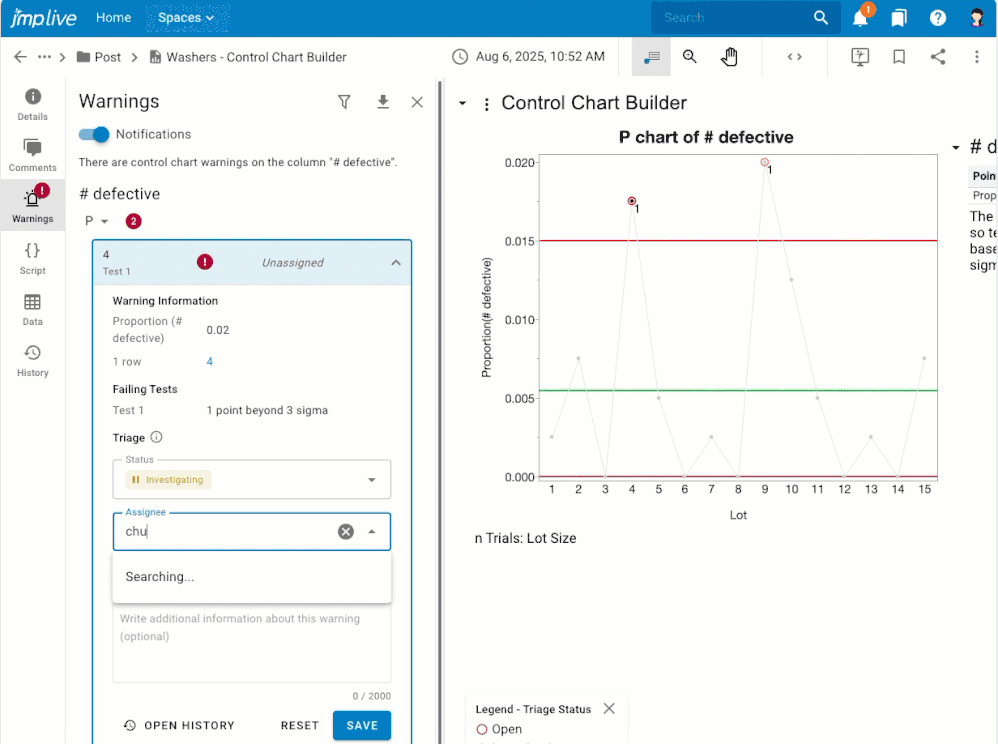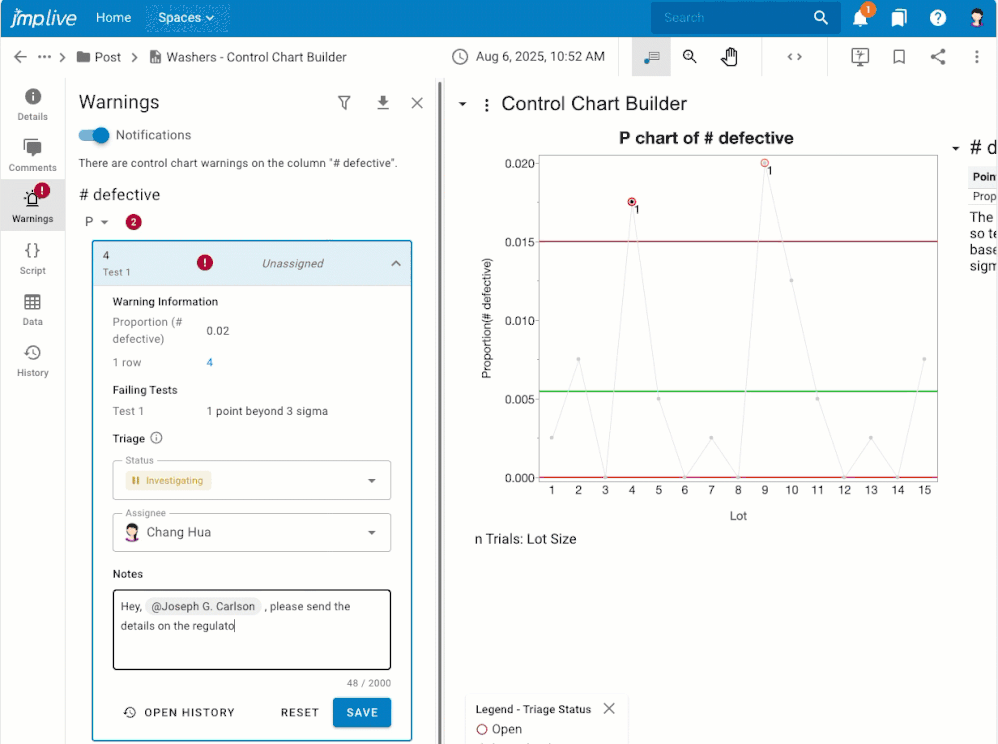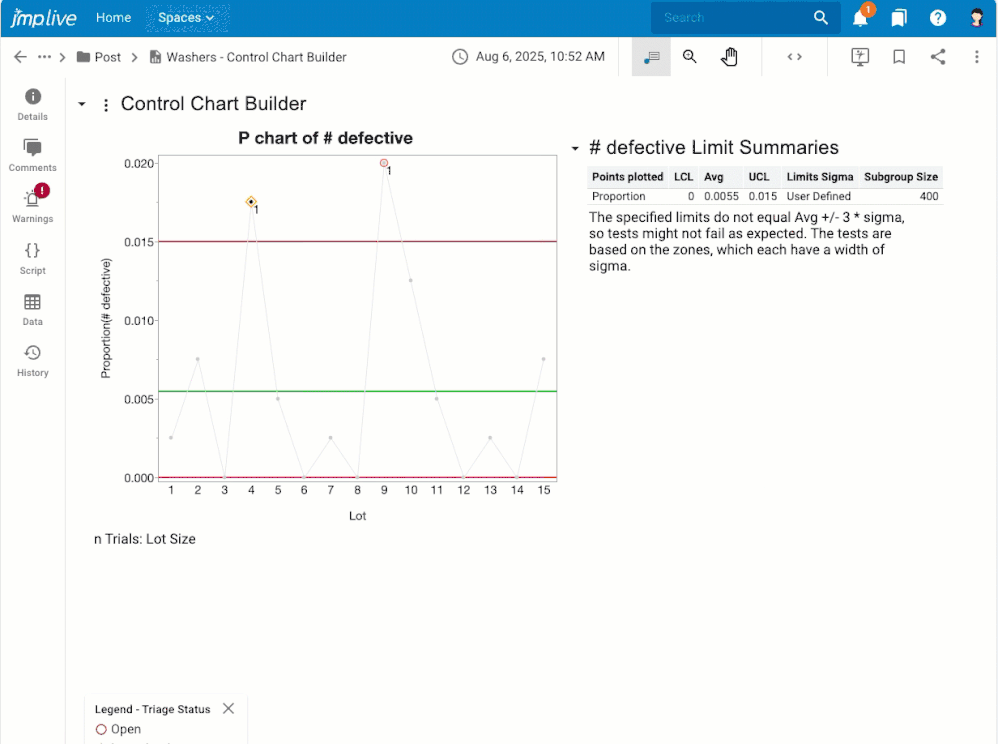
Overview If you have control chart warnings, you may want to: Get notifications about warnings that nobody has investigated yet.Assign warnings to another user, or to a user group, for investigation.Stay on top of the warnings that are assigned to you for investigation.Stay focused on the processes that still need attention.Know what happened, who dealt with it, and when by reviewing and downloadi...
 Aurora_TiffanyD
Aurora_TiffanyD

Every pharmaceutical manufacturer needs to monitor its manufacturing facilities for possible contaminants from the environment. Mold from airborne spores and bacteria on surfaces are two of the threats that can ruin a batch. Other kinds of factories, like in the semiconductor industry, are threatened by airborne particulates. These facilities have specialized collection devices for environmental m...
 John_Sall
John_Sall
JMP has long been a leader in providing the statistical tools needed by engineers and technicians to measure and analyze variations in the quality of products and the processes that produce them. These tools include: Control charts provide feedback on key variables and show when a process is in, or out of, statistical control. The Control Chart Builder platform provides an interactive, point-and-c...
 Eric_Hill
Eric_Hill
Bayesian Optimization, aka BayesOpt, is a new platform coming to JMP Pro 19. With it, you can use your existing data to fit a model and then use that model to intelligently decide where to sample next. These new observations are used to update the model and find even better samples. This process can start with a minimal number of runs, which means wasting fewer resources on suboptimal samples and ...
 Kasia_Dob
Kasia_Dob
