DOE evaluation with random factors ends up with unrealistc results. Why and how this can be avoided?

[#1]

Hallo,

we have run a DOE and monitored some DOE factors (Ta_mes, c_mes) and some additional values that supposed to be stable but have not been so (Tb_mes, random test vehicle).

Modelling gives quite different predictions in case random factors are used for the model or not. They are even unrealistic (negative thicknesses s-2, or very high TE (higher than during the trials)).

see for example the Profiler HSS-TE versus HSS_random

Do you have any explanation why this is happening and how to avoid?

General explanation:

The DOE was designed with 8 whole plots and 16 subplots. The whole DOE was run in one tank. The wholeplots represent different plating days, and subplots the daily temperature increase (unfortunately cooling down would take to long - therefore the temperature Ta increase was always positive despite the original design). A third irreversible change (concentration increase c_set) was marked as block during design augmentation.

Results are on the right side of "Y".

[#2]

I do not understand your description of the experiment or the problems with your analysis.

I started over with the analysis. Several factors and responses had the wrong data type, wrong modeling type, and were missing valuable column properties. I restored all the data columns to their best state. I deleted all the saved table scripts, summary statistics, and saved prediction formulae. I then had no trouble fitting reasonable linear models with the random effects. Peeling had no significant effects.

I attached my version of the experiment and analysis for your examination.

[#3]

Dear Mark,

thank you for looking into this.

I will try to clarify:

Unfortunately responses (s-2, s-1, Peeling, HSS-TE, HSS-SS, LM-void) have not been specified, when the DOE was set. Therfore, the Y column is empty.

During each run of the experiment a test vehicle was plated.

First, the plated thickness (s-2 (numeric/continuous), s-1(numeric/continuous)) was measured.

From previous tests we know, that the temperature Tb with slight alternations has an impact on the thickness s-2 (Mean(s 2 (µm))). Therefore, the temperature Tb_mes was determined for each run and used as a random factor during modelling of s-2.

And in this case we ended up with negativ predictions for the thickness. Why?

Second, a tape test was done on one part of the test vehicle with the result: peeling(character/ordinal).

Third, another part of the test vehicle was used for a soldering test with the results: HSS-TE (numeric/continuous), HSS-SS (numeric/continuous), LM-void (character/ordinal).

From previous test with s-2 thickness variations we know that the soldering test is influenced by the thickness s-2. Therefore the thickness s-2 (Mean(s 2 (µm))) was used as a random factor during the evaluation of the soldering results, e.g. HSS-TE.

In this case we ended up with HSS-TE predictions that were much higher than without random factor, even higher than the results (see Actual by Predicted Plot). Why?

PS: According to the JMP message "Random ettects are not supported by Ordinal Logistic". Therefore the modelling was done without random factors for Peeling and LM-void. Or is there a way to include random effects for results with modelling type character/ordinal? 

I hope this explanation helps to clarify.

Best regards

Petra

[#4]

Did you examine the analysis I performed? Did my approach make sense? Did the results make sense? I still do not understand your analysis. Details:

• Regarding the effect of Tb on s-1 and s-2, I do not understand what you mean by "used as a random factor." Do you mean that you modeled Tb as a random effect?
• Negative predictions are possible in general because of the linear model. It assumes that the response varies from negative infinity to positive infinity. Also, the error contribution is modeled as a normal distribution with a mean zero so half the errors are negative, too. It is difficult to answer your question because you have not shown the model that was used or the regression analysis results.
• Peeling appears to be a class indicated by a number so I changed it to numeric / continuous to fit a model.
• s-2 is a "random factor?" I do not know what that statement means.
• Predictions are based on a model. Always. If you do not include the factor, then the model is the mean response plus the error. If you do include the factor, then it is possible for the mean to vary and be higher (and lower) than without a factor.

[#5]

I looked at my analysis again and realized that you have an important inconsistency between what you specified in the design and what you actually did in the experiment.

• You do not need Block in the model as it is confounded with Whole Plots and Subplots, c set, and (mostly) Tb set..
• c set is not specified in the design as a factor. How was it added to the augmented design?
• c set is at the same level in Whole Plots 1-4 and again at the other level in Whole Plots 5-8. Was it really only set and reset once? Was it constant in the first 16 runs and then added to the experiment at a constant second level?
• Was Tb added to the experiment like c? It doesn't seem to be a design factor but another variable added after the experiment was designed.
• You have a hard to change factor Ta. It should be set and held at one level within the entire subplot. Yet you have different values for Ta mes. It seems that the measure variable indicates control within a run and Subplots indicates random error from setting the hard to change factor so I left Subplots in as a random effect and Ta mes as a fixed effect in place of Ta set.

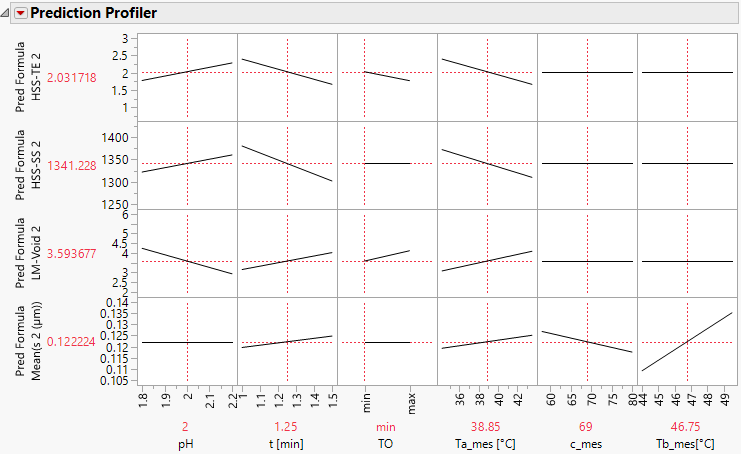
I updated my analysis and saved the new Model script in the attached data table. I obtain the following profiler after completing model selection and saving the preediction formula for the four responses with significant effects.

[#6]

Dear Mark,

the tests were done in a vessel/tank and concentration cset changes are irreversible in a vessel/tank.

You are right, the concentration c was constant during the first 16 runs, than increased and again constant during run 17-32.

To implement the concentration into the model a column cset was added to the original data table. If I do it the correct way as constant I end up with a constant, therefore I temporarily changed one value to the higher concentration before model augmentation and "corrected" it afterwards.

I did no see a different way as blocking during augmentation to implement the concentration cset into the model, because the whole plots and subplots were needed already to discribe the temperature Ta and pH change. Both was done blockwise, because otherwise changes would consume too much time.

• pH adjustment needs to be done at room temperature (before heating). -> Each day only one pH set can be tested.
• Heating (and cooling) of the vessel/tank takes time. To have at least 4 runs a day, only one temperature Taset increase was done daily. 

The temperature Tb should be constant, but in fact it is not. therefore it was measured simultaneous for each individual run. It is an random factor that was added as column afterwards.

The temperature Ta I handled in the same way as you.

.....

I'am struggling to find a way to insert (copy/paste) parts of the jmp analysis. I will continue to explain when I find I way.

[#7]

Thanks for the update but I am now unsure where you stand with the issues. Do you still need help?

[#8]

Dear Mark,

Yes - please.

Attached please find a Journal with different modells for s-2 and TE. For me it is very unclear why I end up with an offset when using additional random factors as e.g Tb_mes for s-2 or s-2 for TE.

[#9 · Accepted solution]

Do not enter factor effects as random effects. The "offset" is an artifact of the miss-specified mixed-effects model that you entered.

You seem to be confused about the nature of fixed effects and random effects. The only random effects in your model should be Whole Plots and Subplots. (The Residual random effect is automatically estimated from the model-dependent squared error and degrees of freedom. It should not be explicitly specified.) The factors, on the other hand, have fixed effects that are reproducible. These effects might require more than one term to be adequately represented: a first-order term, a second-order term, or crossed term. For example, your factor Ta should produce a fixed effect. The data column Ta is used to produce estimation columns for the regression model such as Ta or Ta^2. The fact that you use the measured level (Ta mes) instead of the original setting (Ta set) does not change the fact that all the Ta terms represent fixed effects.

Usually a designed experiment is associated with a hypothesized model that is estimated and tested. I have already responded more than once with reasonable models for your experiment and data.

[#10]

Yes, you are right: I thought, that factors that have not been designed and that should be fixed, but in reality are not, would get the attribute "random effect" during modelling.

Would it make sense to set the design role to "noise" for these semi-fixed unplanned factors, to take into account that it cannot be assured that the variation will be independent to other factor changes (risk of coincidentially correlations)?