- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: effect of centre points
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
effect of centre points
Hello:
It is mentioned that adding centre point in the DOE will help in understanding if there is any curvature effect. But those points will not help you know which factors are the source of this nonlinearity (see below image)
I have some questions based on this
Q1) What parameters should we look in the analysis to see if there is a curvature effect?
Q2) If we find out that we have curvature effect, do we have to run the entire experiment again with three factor levels? or just run the additional experiments at the middle level for all the factors?
Q3) Is there a way to identify which factors might be contributing to the curvature, or it is just the domain knowledge question?
Your help is highly appreciated.
Best Regards,
Varun Katiyar
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: effect of centre points
Hi @VarunK,
I won't answer specifically at your questions since @statman did a great job at answering them.
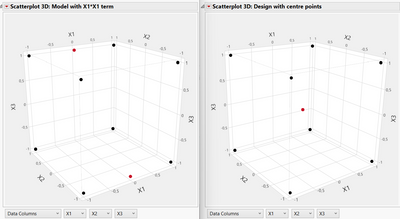
However, one precision about question & answer 1) : If you add the quadratic effect A*A, it won't add a centre point in the design, but (one or) several points in the middle of the range for the factor A (see capture below : on the left, a custom D-optimal design with the term X1*X1 added, so two points (in red) with X1=0 added in the design. On the right, I specifically added centre points (in red) in the custom design).
The information from these diverse points is different, so you won't be able to test curvature "in general" by adding specific quadratic terms, you will be able to do it only for the factor(s) for which you added a quadratic term (you have no information or possibility to test for potential curvature effect for factors B and C if you only have points at level 0 for A).
The decision to use centre points or "middle" points (aimed at estimating specific quadratic effects) depends on the objective you have, which design phase you're in (screening / optimization / prediction / robustness), your experimental budget and your domain expertise.
The centre points are commonly used for two main purposes :
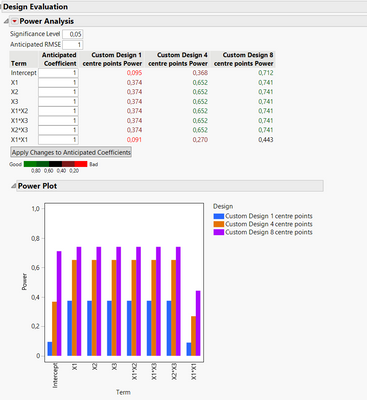
- Estimate pure error for the lack-of-fit test, to evaluate if you model seems adequate.
In order to have sufficient power for this lack-of-fit, several centre points (replicates) may need to be done (example here with 3 designs, with 1 to 8 centre points added with quadratic effect X1*X1 power evaluation). -
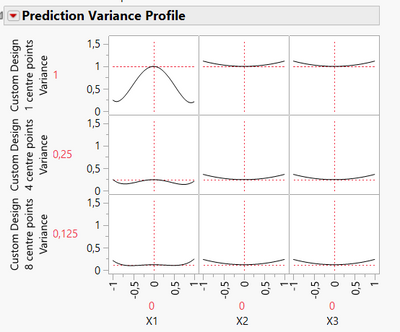
Decrease variance prediction in the centre of the experimental space.
This is particularly useful, as your design may often be centered on the initial settings/prior knowledge you have (and factors you want to investigate), so it may be reasonable to have a low prediction variance in this area.
For robustness studies, this is even more important, as the centre points reflect the optimal settings you already have identified and predicted, and the goal is to make sure small variations around this optimum can be handled (or have little to no influence on the outcomes). So you may need the lowest prediction variance possible in the centre of your experimental space when running a robusness study, to make sure small changes are not significant. Example here with the same 3 designs with increasing number of centre points (1, 4 and 8) and their impact on prediction variance :
As you can see, centre points can be helpful in several situations. The decision to add/use them depends on several parameters and also on the model and type of design : optimal design may not require centre points if you already have specified quadratic terms as "Necessary" or "If Possible", but classical designs like Central Composite Design do need them.
You can read some of these ressources for more info :
https://online.stat.psu.edu/stat503/lesson/11/11.2/11.2.1
https://www.statease.com/blog/importance-center-points-central-composite-designs/
I hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: effect of centre points
Here are some thoughts:
1. To test for simple curvature (or departure from linear), you should add one quadratic effect to the model (1 DF). If you have factors A, B and C, add A*A. Note that A*A = B*B = C*C, hence your quadratic effect cannot be specifically assigned.
2. If the quadratic effect is significant both practically and statistically, then you will need to iterate to determine which factor(s) are responsible. I believe this starts with subject matter expertise and hypotheses. Then design the next experiment. While it is one option, I would not simply add the "third" level to each factor as you confound block effect with the quadratic term estimates. You also have the option of using augment design and have JMP suggest additional runs. These also have the potential of confounding with block effects. You could move the space (change factor levels) for the next iteration in the direction of improvement, drop insignificant factors and add additional levels.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: effect of centre points
Hi @VarunK,
I won't answer specifically at your questions since @statman did a great job at answering them.
However, one precision about question & answer 1) : If you add the quadratic effect A*A, it won't add a centre point in the design, but (one or) several points in the middle of the range for the factor A (see capture below : on the left, a custom D-optimal design with the term X1*X1 added, so two points (in red) with X1=0 added in the design. On the right, I specifically added centre points (in red) in the custom design).
The information from these diverse points is different, so you won't be able to test curvature "in general" by adding specific quadratic terms, you will be able to do it only for the factor(s) for which you added a quadratic term (you have no information or possibility to test for potential curvature effect for factors B and C if you only have points at level 0 for A).
The decision to use centre points or "middle" points (aimed at estimating specific quadratic effects) depends on the objective you have, which design phase you're in (screening / optimization / prediction / robustness), your experimental budget and your domain expertise.
The centre points are commonly used for two main purposes :
- Estimate pure error for the lack-of-fit test, to evaluate if you model seems adequate.
In order to have sufficient power for this lack-of-fit, several centre points (replicates) may need to be done (example here with 3 designs, with 1 to 8 centre points added with quadratic effect X1*X1 power evaluation). -
Decrease variance prediction in the centre of the experimental space.
This is particularly useful, as your design may often be centered on the initial settings/prior knowledge you have (and factors you want to investigate), so it may be reasonable to have a low prediction variance in this area.
For robustness studies, this is even more important, as the centre points reflect the optimal settings you already have identified and predicted, and the goal is to make sure small variations around this optimum can be handled (or have little to no influence on the outcomes). So you may need the lowest prediction variance possible in the centre of your experimental space when running a robusness study, to make sure small changes are not significant. Example here with the same 3 designs with increasing number of centre points (1, 4 and 8) and their impact on prediction variance :
As you can see, centre points can be helpful in several situations. The decision to add/use them depends on several parameters and also on the model and type of design : optimal design may not require centre points if you already have specified quadratic terms as "Necessary" or "If Possible", but classical designs like Central Composite Design do need them.
You can read some of these ressources for more info :
https://online.stat.psu.edu/stat503/lesson/11/11.2/11.2.1
https://www.statease.com/blog/importance-center-points-central-composite-designs/
I hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: effect of centre points
Thank you Victor for taking out time and replying in detail.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us