- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Just love it when R2 comes out negative
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Just love it when R2 comes out negative
Hi all,
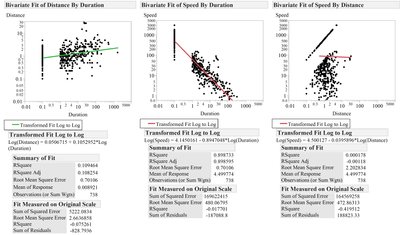
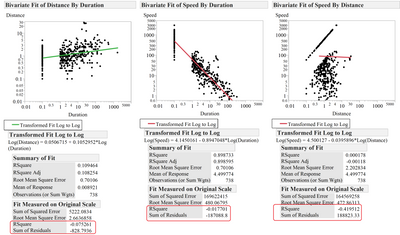
Does anyone know what JMP does in the bivariate fit platform when calculating the “fit measured on original scale”? I just got a negative R2. Does it estimate a model without the intercept?
I know the data is peculiar and when using the log-log transformation I have many missing observations but still, something must be going on....
Attached is the data table with a script to reproduce the results I got.
Thanks,
Ron
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Just love it when R2 comes out negative
Two modes, one fit to the original data and the other to the log-log transformed data, are different models. Anti-logs won't make summary of fit statistics from the log linear model identical to the results from the original linear fit.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Just love it when R2 comes out negative
Your R Square is actually positive, but it is close to zero. When this happens, adjusted R square maybe slightly negative. This is how adjusted R square formula is built to work. In fact, if R Square is <k/(n-1) , R Square Adj will be negative.
In your case, a negative R Square Adj. will occur when R Square <0.0013568. What a negative R square Adj. means is that the model terms do not help predict the response.
Does it estimate a model without the intercept?
No, it includes an intercept by default.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Just love it when R2 comes out negative
I would add that what a negative R Square Adj means is that the portion of variability of the predictors do not help predict the expected response. Thus, the R Square should not be used exclusively as the iron-fist to judge a model's anticipated performance. But it is also good for the R Square and the associated R Square Adj. to be positive.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Just love it when R2 comes out negative
thanks for the comment jiancao
I must be missing something. where exactly does it say adjusted in the output?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Just love it when R2 comes out negative
R Square Adj is the original R^2 adjusted for # of model terms in regression
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Just love it when R2 comes out negative
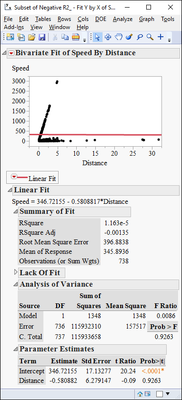
sorry for the misunderstanding. i was referring to the R2 marked below.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Just love it when R2 comes out negative
My apologies for missing the Fit Measured on Original Scale report. The attached table show where a negative R Square came from in this case. I saved the column Residuals Speed from the model fit (Notice that that it is calculated by taking Exp to back transform to the original scale). Then I calculated two Sum of Squares columns: SS of Total (SST) and SS of Error (SSE), for the R Square formula used by JMP, which is 1- SSE/SST=1- 164569257/115933657=-0.41951234. So, the back transformation gives rise to a negative R Square.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Just love it when R2 comes out negative
Thank you jiancao,
that did reproduce the negative figure. yet i would expect the figure to be identical to the outcome of fitting a line to the same data as in the picture.
but if i just run this with a fit line i do not get the same R2.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Just love it when R2 comes out negative
Two modes, one fit to the original data and the other to the log-log transformed data, are different models. Anti-logs won't make summary of fit statistics from the log linear model identical to the results from the original linear fit.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Just love it when R2 comes out negative
I see, so how can i make use of the anti-log results? what are they comparable to?
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us