- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- How to interpret the results from a paralellism test of two non linear curves - ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How to interpret the results from a paralellism test of two non linear curves - F test
Hi
I need to prove, statistically, that these two curves are parallel. I have made a data table, fit a non linear 4PL curve and ran a parallelism test. Unfortunately my statistical knowledge is limited and I don´t know how to interpret the results. I would assume since the Prob value of the F test is below 0,05 the result is significant and therefore the null hypotheses is correct and and the lines are parallel. However the Prob value shows up orange, which confuses me.
Could someone help me make sense of this? And also explain the importance of the Prob ChiSq.
Thank you :)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to interpret the results from a paralellism test of two non linear curves - F test
Good question. But, you have it backwards. If p-value < 0.05 then there is evidence of non-parallelism. You're testing the null hypothesis of equal lower and upper asymptotes and slopes. To that end, either an F or Chi2 test statistic is used. Lack of statistical significance (p > alpha) at a preselected level (alpha=0.05, for example) is viewed as indicative of parallelism (i.e., can not reject the null hypothesis). Conversely, if p < alpha then then the hypothesis of parallelism is rejected.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to interpret the results from a paralellism test of two non linear curves - F test
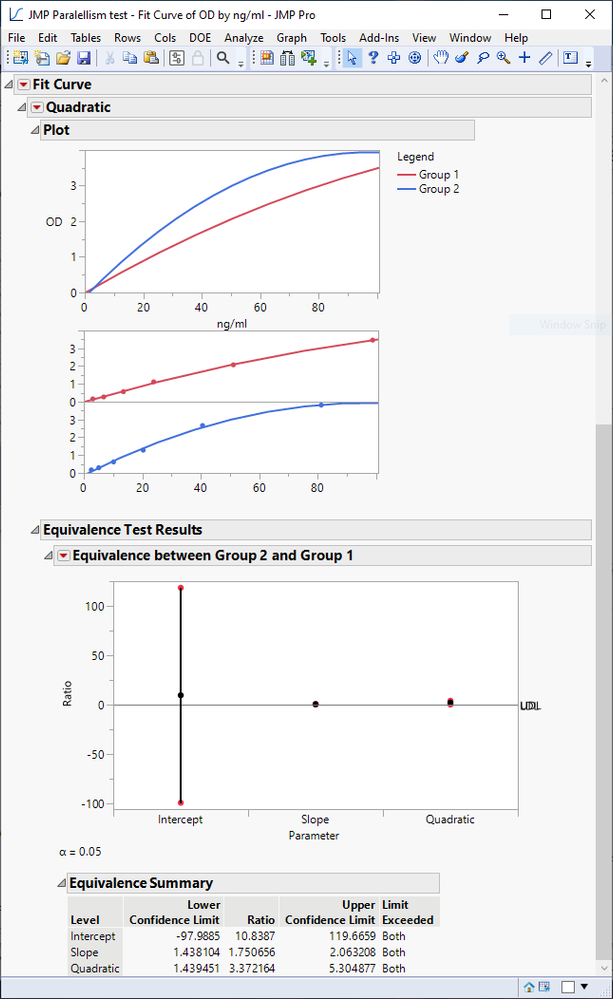
The example you shared will be poorly modeled by a 4PLC. You have observed a narrow range that does not exhibit the four features of a sigmoid curve, so it is difficult to estimate all four parameters well. A quadratic polynomial will be better.
Also, parallelism tests are provided for compatibility. They are legacy tests that are still commonly used today, but they are indefensible. An inferential test works in one direction only. They are used to establish the alternative hypothesis with data. The parallelism tests use an alternative hypothesis that there is a difference. Failure to reject the null hypothesis (i.e., they are parallel) cannot be used as an argument for parallelism. It is invalid. You must use inference where the alternative hypothesis is an equivalence (parallel) and reject the null hypothesis that they are different (non-parallel) to conclude parallelism.
The equivalence test fails, as expected by inspection of the plot of the data and the fits. They do not have the same shape.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to interpret the results from a paralellism test of two non linear curves - F test
Hi Mark: Thanks for introducing the Fit Curve platform to me! I had no idea of its existence. It is a great set of tools, and is a great addition to JMP!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to interpret the results from a paralellism test of two non linear curves - F test
Thanks for the reply Mark.
I can see the mistake in choosing a 4PL as the curve does not have the sigmoidal shape. Noted, actually look at the shape of your curve! I am learning.
Regarding the equivalence test, it fails because all factors (intercept, slope and quadratic) are out of limit? Would it fail if only the slope is within limits? Could you give further instruction on how to interpret the results of this test?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to interpret the results from a paralellism test of two non linear curves - F test
In the case of the quadratic example, for parallelism slopes and quadratics must be equivalent. So, to answer your question, yes it would fail if only the slope is within limits. The difference in intercepts is an offset between the two curves, so it has no effect on parallelism.
A pretty good discussion is here.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to interpret the results from a paralellism test of two non linear curves - F test
What does it mean to be parallel? It means the same shape but a shift left or right from the standard curve. So one parameter can vary, but the others must remain 'fixed.'
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us