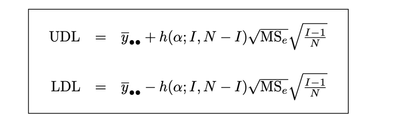- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: ANOM JMP v's Wheeler
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
ANOM JMP v's Wheeler
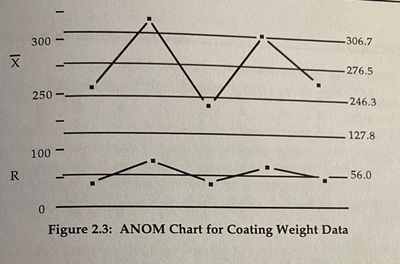
Hi I am trying to replicate an ANOM that Wheeler did in Understanding Industrial Experimentation p60 (details attached)
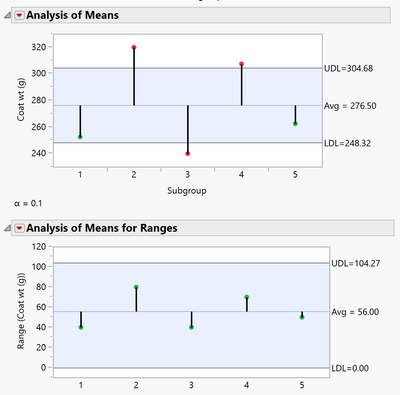
I have attached the data set, I get different control limits for some reason, I set the alpha level at 0.10
Can you advise
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: ANOM JMP v's Wheeler
The JMP help notes that JMP implements the methods from Nelson, et. al (2003). link to JMP ANOM help
The methodology in the Nelson book differs slightly from Wheeler's, for instance the measure of error differs. Therefore, the ANOM decision limits calculated in JMP will differ from those in the Wheeler book. You can find the Nelson ANOM book here (ANOM Book ).
For the equal case for means the decision limits are:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: ANOM JMP v's Wheeler
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: ANOM JMP v's Wheeler
The JMP help notes that JMP implements the methods from Nelson, et. al (2003). link to JMP ANOM help
The methodology in the Nelson book differs slightly from Wheeler's, for instance the measure of error differs. Therefore, the ANOM decision limits calculated in JMP will differ from those in the Wheeler book. You can find the Nelson ANOM book here (ANOM Book ).
For the equal case for means the decision limits are:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: ANOM JMP v's Wheeler
Thanks Karen, I asppreciate your response here
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: ANOM JMP v's Wheeler
Hi Karen, I just looked at the book, your one of the the authors. So which is the best method and why ;0)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: ANOM JMP v's Wheeler
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: ANOM JMP v's Wheeler
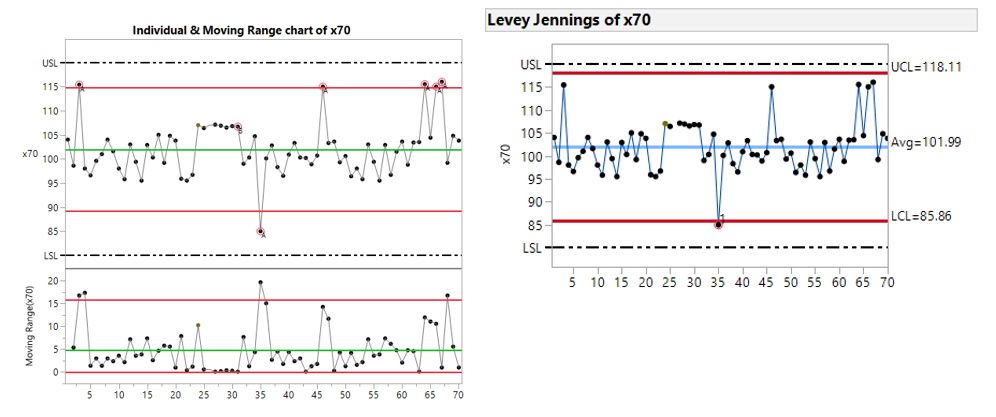
Thanks, that really helps understanding the difference. I have dealt with SD and ranges with the control charts. The Shewhart chart and the Levey–Jennings charts for calculating control limits, where the Levey–Jennings uses SD. Its important to understand these differences.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: ANOM JMP v's Wheeler
Another important distinction between Shewhart charts and Levey-Jennings charts is that the former types rely on short-term variation that is internally estimated in Phase I. The latter type often uses externally determined long-term variation. A clinical laboratory scenario, from which they originated, is given the SD or control limit information by the manufacturer of the assay, which they base on a precision study that intentionally includes long-term variation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: ANOM JMP v's Wheeler
Hi Mark
I must admit I do struggle with Levey-Jennings charts. When the process chart is stable the control limits equate to Shewhart chart limits, but when the process is not in control (as mesured by the Shewhart chart) the control limits are more forgiving (wider). Now I undertand that the Westguard Rules should then kick in, but very often people do not use these Rules, so the sensitivity of the Levey-Jennings chart is diminnished. A Strong signal becomes a Weak signal. The standard deviation component of the Levey-Jennings chart assumes the data is consistent, stable and attempts to fit these wider control limits to all the data.
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us