On a recent vacation day, I had promised my daughter that we would do an experiment together. While we’ve done some experiments from kits that we’ve picked up in retail stores, I’ve been wanting to get back into doing some home experiments with JMP, and was particularly inspired by recent posts from my colleagues @Peter_Hersh (cycling) and @Peter_Polito (running).
I had recently set up a 6-lane racetrack for diecast cars that I’ve had tucked away for several years. We decided to have my daughter pick a subset of her favorite cars and try to discover who the fastest racer is. While there may be more sophisticated setups that measure the timing between start to finish, all we have available to us is the lane number of the winner, so our “fastest” is really a measure of which car is most likely to win.
My daughter picked 10 cars that we were going to race with. Her picks also happened to coincide with character cars from a production company, and she was very keen on seeing if a pair of princesses (one with magical ice powers) would be crowned the champion.
With our cars picked, it was time to design an experiment. There are a few different issues to think about in designing this experiment:
- We can only use at most 6 of the 10 cars at any time.
- The Lane Number may be important, so we want to try to take it into account.
- Our response is who the winner was out of a given group of cars.
Thinking about issue 1, it seems reasonable to treat these “race groups” as blocks of size 6. When also accounting for issue 2, we want to spread out the cars to different lanes among the blocks. Ideally, we can also race each pair of cars against each other at some point in the experiment in one of the sets.
To handle the response, we don’t have a continuous response. Treating it as binary (win vs. loss) is not quite right, since we’re not accounting for the block structure. But, if we think of the winner as a “preferred choice” from the group of 6, we can analyze this experiment as a choice experiment, where the car and lane number would be the effects that we want for estimating the utility.
After some thought, it seemed like a balanced incomplete block design (BIBD) analyzed as a choice design would be a reasonable choice. The BIBD platform can be found under:
DOE->Special Purpose->Balanced Incomplete Block Design
Our “Treatment” here is the car, so I change the name to “Car” and enter the 10 different cars we’re using:
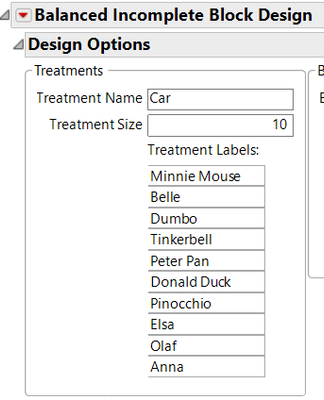
If we put in a Block Size of 6 (i.e., 6 cars at a time), we can get a design with 15 blocks. Even if running the same 6 cars multiple times, 15 configurations seemed doable with a 5-year-old. We could have saved a few sets of races by using 9 or 11 different cars, but we already had 10 picked out.
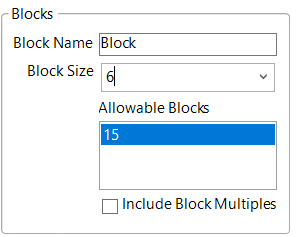
Clicking the “Make Design” button, and looking at the Diagnostics under “Incidence Matrix”, we can get an idea of the properties of the design.
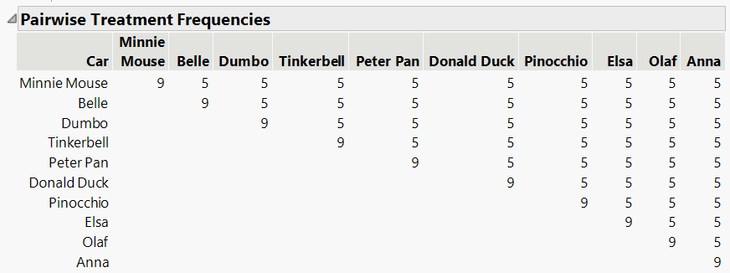
The “Pairwise Treatment Frequencies” indicate that each car will be used 9 times, and will appear in a race against each other car 5 times:
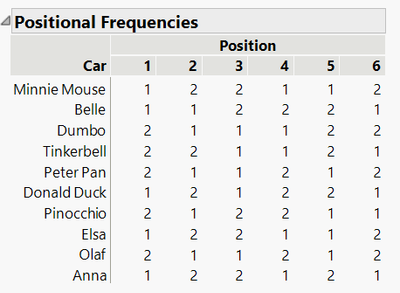
Many of the designs in the BIBD platform have been optimized for the positional frequencies. In this case, the position would reflect the lane number, so we do want to ensure that these are as balanced as possible. We cannot achieve perfect balance, since each car appears 9 times (which is not divisible by 6), but the positional frequencies are as balanced as possible, which is what we want:
Note that way back in the “block size” step, there was a checkbox for “Include Block Multiples.” Since we were planning to run each block multiple times, we could have used this to rearrange the position of the 6 cars in a block for each race. I ultimately decided against this, since it was much simpler to just keep the cars in the same lanes when running replicate races of a block.
Stay tuned for the results. Who are you cheering from our list? Please let me know your favorite in the comments. Thanks for reading!