Why there are no confidence interval for orthogonal regression

[#1]

Hi all, 

I just have a question when using fit Y by X function in JMP. 

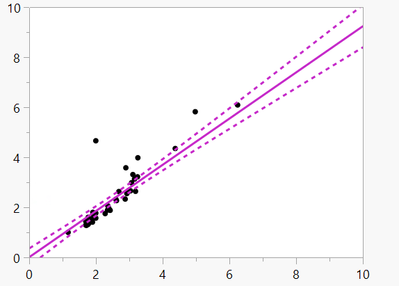
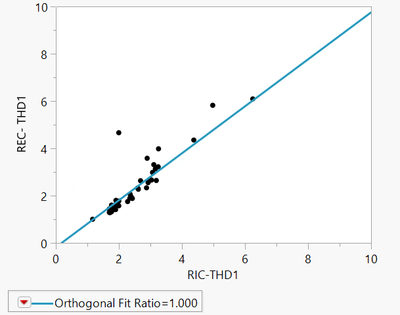
I use 2 method is linear regression & orthogonal regression for a data.

I know the difference is Linear method assume that there is only variations at Y value when Orthogonal assume variation of both X,Y. 

But I wonder why can't I draw the  Confidence interval or prediction interval in the orthogonal method. 

I just can see the Lower CL & Upper CL & cannot draw the line. 

is this Lower & upper CL is confident interval? 
If yes can I somehow draw the CI into the chart? 

Can somebody help to explain? Thank you very much

[#2]

By a quick search on Internet, I don't see definitions for confidence intervals or prediction intervals of a fitted orthogonal regression.

Here is my view. If one would like to define something similar to what is available for OLS, e.g. intervals given X, the definitions may not exist for orthogonal regression. Because one needs to know the distribution of Y given X. I don't see that distribution is immediately available.

On the other hand, if it is reasonable to think differently, a different definition may bring something a little bit more useful. How about a "bootstrapped confidence interval"? I.e. fit the orthogonal regression on bootstrapped samples again and again, collect all fitted orthogonal regression lines. The result should tell you something about the uncertainties involved in the fitted orthogonal regression.