- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- When should you not use predictor screening?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
When should you not use predictor screening?
I'm curious if there are any times when you should not use the predictor screening tool, & if so, what should you check with your data to understand if you might have issues using predictor screening?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: When should you not use predictor screening?
I find predictor screening immensely valuable, but like any automated tool it can't account for some things. It is most valuable when you have many potential predictors - however, when these predictors are closely related, I don't quite trust the automated procedure. I find this to be a common problem, where I have data sets that have a number of closely related measures (for example, hotel availability at a number of different time points). If you just use predictor screening you may get the single most closely related one of the measures or possibly a number of them will be chosen. Or, potentially none will stand out (I'm not sure about that one)? What I do in such cases is manually analyze the closely related predictors, using the Multivariate platform. I can then choose one of the related measures to use in predictor screening.
There are other more complicated cases. Predictor screening will not identify if you should create new variables as functions of existing ones (such as ratios of two measures). It will not give you a good idea whether you should recode some of your nominal variables (I'm not sure about this one either - I haven't experimented to see). In general, I'd say that Predictor Screening does not replace all of the normal data cleaning steps - it is most valuable when used after cleaning the data.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: When should you not use predictor screening?
Hi @mjz5448,
I might add a complementary answer to elucidate some of the informations given, based on the previous responses I have already written on similar topics:
Predictor Screening is a method based on the Random Forest algorithm that help you identify important variables (identified by the calculation of features importance) for your response(s) in your historical data. Depending on the representativeness of your data, coverage of the experimental space, missing values, presence of outliers, interactions, correlations or multicollinearity between your factors, this platform may have some shortcuts, many unknowns, and shouldn't be trust blindly (as stated by @dlehman1).
- The analysis and insights you can have with this analysis is only limited to the historical experimental space (which might be too limited and/or not representative for a good understanding of the system). You can see this as Production experimental space (historical data) vs. R&D (DoE) : in production, only small variations of the factors is allowed (and some are fixed, so you won't be able to determine their importances) to create robust and quality products, whereas in R&D the objective is different : explore an experimental space and optimize the factors of a system, by using larger ranges for the factors considered.
- The Predictor screening platform doesn't give you a model (unlike the Bootstrap Forest available in JMP Pro), only feature/factor importances, so you don't have access to individual trees and branches, which could help identify interactions between factors, and the threshold levels values of factors used for the splits.
- Since you don't know the quality of the model behind (through R², RMSE or other relevant metrics according to your objectives), you don't know how much variability is explained through it (or how accurate the model is) and if the calculations of feature importance is relevant/adequate for your topic.
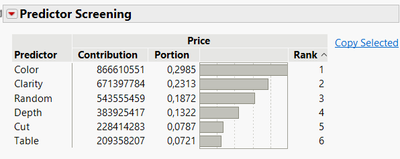
- Since all factors are ranked, the threshold/limit between important and non-important factors is not trivial. To help you with, you can add a random factor (with random values). An example of this technique is shown here with the Diamonds Dataset from JMP with Price as response, adding a random factor and omitting Carat Weight as possible input (since it is a very important predictor, so I wanted to show you an example where it's hard to sort out the other predictors) :
- This platform doesn't give you indications about possible correlations or multicollinearity between factors. You can use the Multivariate platform to explore correlations between inputs, outputs, and input-outputs. You can also create dummy regression models to calculate VIF scores between your factors, in order to spot multicollinearity.
- High cardinality categorical factors may also bias the feature importance calculations. The more cardinality (number of classes), the higher the bias, as the data will form a high number of small groups/classes that the model will try to learn. So it will fail to generalize or "understand the logic" and as a result this will increase the chance of overfitting, giving this feature a high importance.
An example here with the same dataset, same conditions but adding a random categorical factors with 11 levels (from A to K, named "Shuffle[Column10]). This categorical random feature with high cardinality is ranked higher than the random numerical variable seen before :
Concerning your questions about multicollinearity :
- The multicollinearity among variables is handled in Random Forest by the random feature subset selection at each node: at each node, to determine the next split, you randomly create a subset of your features and evaluate in this subset which feature (and at which threshold level) is able to separate best the data points based on their response values. So as every feature has equal chance to be selected, even correlated features can be selected and have a similar feature importance in the model. This process minimize the impact of correlation between columns, and is not present for Decision Tree (or Boosted Tree), where a single tree is created with all features tested at each node : only one of the correlated features might be selected for the split.
- Since Random Forest creates a big model based on many decision tree trained in parallel on bootstrap samples, each individual tree is trained on a slightly different dataset, which also help reducing the correlations between each trees (correlations between rows) and reduce model variance.
More infos on tree-based models :
And about the advantages of Random Forests : https://www.linkedin.com/posts/victorguiller_doe-machinelearning-randomforests-activity-712755779981...
Hope this complementary answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: When should you not use predictor screening?
I find predictor screening immensely valuable, but like any automated tool it can't account for some things. It is most valuable when you have many potential predictors - however, when these predictors are closely related, I don't quite trust the automated procedure. I find this to be a common problem, where I have data sets that have a number of closely related measures (for example, hotel availability at a number of different time points). If you just use predictor screening you may get the single most closely related one of the measures or possibly a number of them will be chosen. Or, potentially none will stand out (I'm not sure about that one)? What I do in such cases is manually analyze the closely related predictors, using the Multivariate platform. I can then choose one of the related measures to use in predictor screening.
There are other more complicated cases. Predictor screening will not identify if you should create new variables as functions of existing ones (such as ratios of two measures). It will not give you a good idea whether you should recode some of your nominal variables (I'm not sure about this one either - I haven't experimented to see). In general, I'd say that Predictor Screening does not replace all of the normal data cleaning steps - it is most valuable when used after cleaning the data.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: When should you not use predictor screening?
Thanks. I also find it pretty invaluable, so I'm wondering where it might fail, & how to check for that failure? I don't know much about the bootstrap forest model that (I think) it's based on, but have briefly read that it's less susceptible to multicollinearity the way linear models are, but have also ready that it could fail if you have linear relationships with the response and predictors, or if you lack iid, but I don't know how you check those assumptions in your predictor screener, or if that is in fact the case as I'm fairly new to these types of data analysis. It would be nice if JMP had a tutorial on what to look for in terms of assumption checking etc..
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: When should you not use predictor screening?
Hi @mjz5448,
I might add a complementary answer to elucidate some of the informations given, based on the previous responses I have already written on similar topics:
Predictor Screening is a method based on the Random Forest algorithm that help you identify important variables (identified by the calculation of features importance) for your response(s) in your historical data. Depending on the representativeness of your data, coverage of the experimental space, missing values, presence of outliers, interactions, correlations or multicollinearity between your factors, this platform may have some shortcuts, many unknowns, and shouldn't be trust blindly (as stated by @dlehman1).
- The analysis and insights you can have with this analysis is only limited to the historical experimental space (which might be too limited and/or not representative for a good understanding of the system). You can see this as Production experimental space (historical data) vs. R&D (DoE) : in production, only small variations of the factors is allowed (and some are fixed, so you won't be able to determine their importances) to create robust and quality products, whereas in R&D the objective is different : explore an experimental space and optimize the factors of a system, by using larger ranges for the factors considered.
- The Predictor screening platform doesn't give you a model (unlike the Bootstrap Forest available in JMP Pro), only feature/factor importances, so you don't have access to individual trees and branches, which could help identify interactions between factors, and the threshold levels values of factors used for the splits.
- Since you don't know the quality of the model behind (through R², RMSE or other relevant metrics according to your objectives), you don't know how much variability is explained through it (or how accurate the model is) and if the calculations of feature importance is relevant/adequate for your topic.
- Since all factors are ranked, the threshold/limit between important and non-important factors is not trivial. To help you with, you can add a random factor (with random values). An example of this technique is shown here with the Diamonds Dataset from JMP with Price as response, adding a random factor and omitting Carat Weight as possible input (since it is a very important predictor, so I wanted to show you an example where it's hard to sort out the other predictors) :
- This platform doesn't give you indications about possible correlations or multicollinearity between factors. You can use the Multivariate platform to explore correlations between inputs, outputs, and input-outputs. You can also create dummy regression models to calculate VIF scores between your factors, in order to spot multicollinearity.
- High cardinality categorical factors may also bias the feature importance calculations. The more cardinality (number of classes), the higher the bias, as the data will form a high number of small groups/classes that the model will try to learn. So it will fail to generalize or "understand the logic" and as a result this will increase the chance of overfitting, giving this feature a high importance.
An example here with the same dataset, same conditions but adding a random categorical factors with 11 levels (from A to K, named "Shuffle[Column10]). This categorical random feature with high cardinality is ranked higher than the random numerical variable seen before :
Concerning your questions about multicollinearity :
- The multicollinearity among variables is handled in Random Forest by the random feature subset selection at each node: at each node, to determine the next split, you randomly create a subset of your features and evaluate in this subset which feature (and at which threshold level) is able to separate best the data points based on their response values. So as every feature has equal chance to be selected, even correlated features can be selected and have a similar feature importance in the model. This process minimize the impact of correlation between columns, and is not present for Decision Tree (or Boosted Tree), where a single tree is created with all features tested at each node : only one of the correlated features might be selected for the split.
- Since Random Forest creates a big model based on many decision tree trained in parallel on bootstrap samples, each individual tree is trained on a slightly different dataset, which also help reducing the correlations between each trees (correlations between rows) and reduce model variance.
More infos on tree-based models :
And about the advantages of Random Forests : https://www.linkedin.com/posts/victorguiller_doe-machinelearning-randomforests-activity-712755779981...
Hope this complementary answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: When should you not use predictor screening?
Thanks Victor_G. I appreciate the insight into multicollinearity - it's not something I typically account for, but will try to do so going forward.
Do you have any insight on whether predictor screening will work if you data is not iid (independent & identically distributed)? I've read that tree-based/random forest models have limitations if your data has a time-series trend, which can be overcome, but that you some how need to transform the data. I'm not sure if that's applicable to predictor screening or not though as I'm just learning about this topic.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: When should you not use predictor screening?
Hi @mjz5448,
Random Forests can be used for time series forecasting (and other algorithms too).
The biggest precaution with non-iid data is to take into account the dependencies/groups in the data, whether it comes from groups of similar observations/individuals, time dependency, measurement repetition, etc...., in your data splitting (training/validation/test). Incorrect data splitting for non-iid data could lead to data leakage, false expectations and over-optimistic results.
Typically for time series forecasting, a specific data splitting for training and validation should be done (not randomly, but more in a "time-window" style), so that the time structure dependency of the responses/data is respected and that there is no data leakage in the setup : no data "from the future" is used in the training that would lead to over-optimistic predictions.
Some reading ressources :
https://machinelearningmastery.com/random-forest-for-time-series-forecasting/
https://mindfulmodeler.substack.com/p/how-to-deal-with-non-iid-data-in
Hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: When should you not use predictor screening?
Thanks Victor_G. I will take a look.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us