- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Understanding Statistical Details for Variance Components
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Understanding Statistical Details for Variance Components
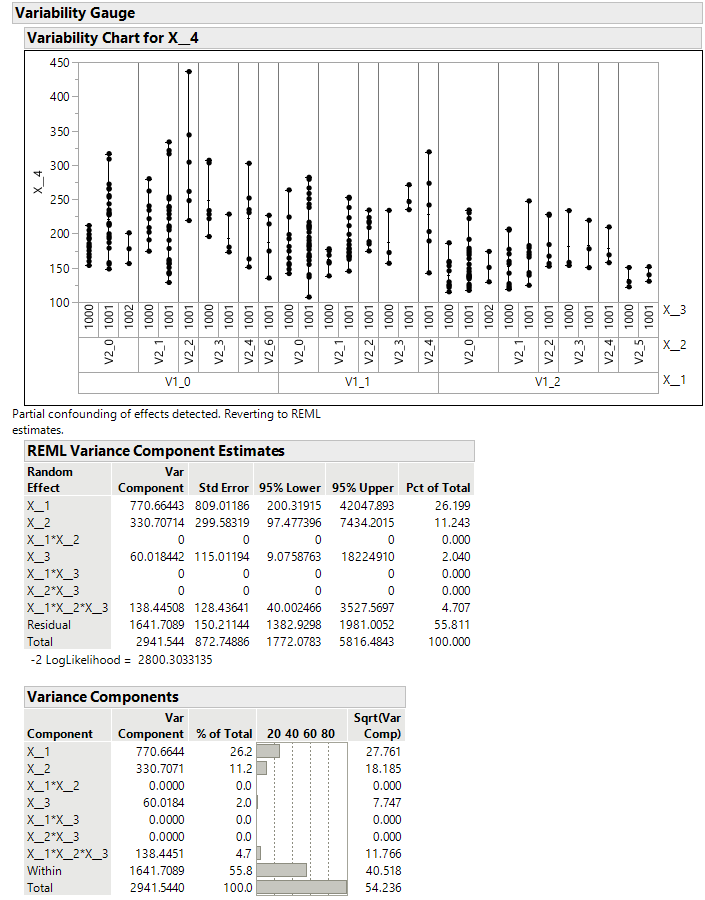
I am working to understand the statistical details for Variance Components platform: https://www.jmp.com/support/help/en/15.2/#page/jmp/statistical-details-for-variance-components.shtml...
For this example, each part is processed within an X_1 group, then within an X_2 group, and then tested within an X_3 group. I think the crossed effects model is most applicable. Is this correct?
More generally, can someone give examples of when to use the Main Effects, Crossed, Nested, Crossed then Nested, or Nested then Crossed models?
New Table( "Variance Example Anonymized",
Add Rows( 273 ),
New Script(
"Variability Chart",
Variability Chart(
Y( :X__4 ),
X( :X__1, :X__2, :X__3 ),
Model( "Crossed" ),
// Analysis Type( "Choose best analysis (EMS REML Bayesian)" ),
Std Dev Chart( 0 ),
Variance Components( 1 )
)
),
New Column( "X__1",
Character( 7 ),
"Nominal",
Set Values(
{"V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0",
"V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0",
"V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0",
"V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_1", "V1_1",
"V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1",
"V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1",
"V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1",
"V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2",
"V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2",
"V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2",
"V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2",
"V1_2", "V1_2", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0",
"V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0", "V1_0",
"V1_0", "V1_0", "V1_0", "V1_0", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1",
"V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_1", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2",
"V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2", "V1_2",
"V1_2"}
)
),
New Column( "X__2",
Character( 16 ),
"Nominal",
Set Values(
{"V2_0", "V2_0", "V2_0", "V2_1", "V2_1", "V2_1", "V2_1", "V2_1", "V2_1", "V2_0", "V2_0", "V2_0", "V2_2", "V2_2", "V2_2", "V2_0", "V2_0",
"V2_0", "V2_3", "V2_3", "V2_3", "V2_1", "V2_1", "V2_1", "V2_4", "V2_4", "V2_4", "V2_0", "V2_0", "V2_0", "V2_1", "V2_1", "V2_1", "V2_1",
"V2_1", "V2_1", "V2_3", "V2_3", "V2_3", "V2_0", "V2_0", "V2_0", "V2_1", "V2_1", "V2_1", "V2_4", "V2_4", "V2_4", "V2_0", "V2_0", "V2_0",
"V2_1", "V2_1", "V2_1", "V2_0", "V2_0", "V2_0", "V2_3", "V2_3", "V2_3", "V2_1", "V2_1", "V2_1", "V2_2", "V2_2", "V2_2", "V2_0", "V2_0",
"V2_0", "V2_0", "V2_0", "V2_0", "V2_1", "V2_1", "V2_1", "V2_4", "V2_4", "V2_4", "V2_0", "V2_0", "V2_0", "V2_3", "V2_3", "V2_3", "V2_2",
"V2_2", "V2_2", "V2_1", "V2_1", "V2_1", "V2_0", "V2_0", "V2_0", "V2_1", "V2_1", "V2_1", "V2_1", "V2_1", "V2_1", "V2_0", "V2_0", "V2_0",
"V2_1", "V2_1", "V2_1", "V2_2", "V2_2", "V2_2", "V2_0", "V2_0", "V2_0", "V2_1", "V2_1", "V2_1", "V2_2", "V2_2", "V2_2", "V2_4", "V2_4",
"V2_4", "V2_3", "V2_3", "V2_3", "V2_0", "V2_0", "V2_0", "V2_1", "V2_1", "V2_1", "V2_1", "V2_1", "V2_1", "V2_0", "V2_0", "V2_0", "V2_1",
"V2_1", "V2_1", "V2_1", "V2_1", "V2_1", "V2_0", "V2_0", "V2_0", "V2_1", "V2_1", "V2_1", "V2_0", "V2_0", "V2_0", "V2_1", "V2_1", "V2_1",
"V2_0", "V2_0", "V2_0", "V2_1", "V2_1", "V2_1", "V2_1", "V2_1", "V2_1", "V2_0", "V2_0", "V2_0", "V2_3", "V2_3", "V2_3", "V2_2", "V2_2",
"V2_2", "V2_0", "V2_0", "V2_0", "V2_4", "V2_4", "V2_4", "V2_0", "V2_0", "V2_0", "V2_5", "V2_5", "V2_5", "V2_3", "V2_3", "V2_3", "V2_2",
"V2_2", "V2_2", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_1", "V2_1", "V2_1", "V2_0", "V2_0", "V2_0",
"V2_1", "V2_1", "V2_1", "V2_1", "V2_1", "V2_1", "V2_0", "V2_0", "V2_0", "V2_6", "V2_6", "V2_6", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0",
"V2_0", "V2_6", "V2_6", "V2_6", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_1", "V2_1", "V2_1", "V2_0",
"V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0",
"V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_0", "V2_5", "V2_5",
"V2_5"}
)
),
New Column( "X__3",
Numeric,
"Nominal",
Format( "Best", 12 ),
Set Values(
[1000, 1000, 1000, 1001, 1001, 1001, 1001, 1001, 1001, 1000, 1000, 1000, 1001, 1001, 1001, 1001, 1001, 1001, 1000, 1000, 1000, 1000, 1000,
1000, 1001, 1001, 1001, 1000, 1000, 1000, 1000, 1000, 1000, 1001, 1001, 1001, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1001,
1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1000, 1000, 1000,
1001, 1000, 1000, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001,
1001, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001,
1001, 1001, 1001, 1001, 1001, 1000, 1000, 1000, 1001, 1001, 1001, 1001, 1001, 1001, 1000, 1000, 1000, 1001, 1001, 1001, 1000, 1000, 1000,
1001, 1001, 1001, 1000, 1000, 1000, 1000, 1000, 1000, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1000, 1000,
1000, 1001, 1001, 1001, 1000, 1000, 1000, 1001, 1001, 1001, 1000, 1000, 1000, 1001, 1001, 1001, 1000, 1000, 1000, 1001, 1001, 1001, 1001,
1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1002, 1002, 1002, 1001, 1001, 1001, 1000, 1000, 1000, 1001, 1001, 1001,
1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, ., ., 1001, 1001, 1001, 1001, 1001, 1001, 1001,
1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1001, 1000, 1000, 1000, 1000, 1000, 1000, 1001, 1001,
1001, 1001, 1001, 1001, 1001, 1001, 1001, 1002, 1002, 1002, 1001, 1001, 1001, 1001, 1001, 1001, 1000, 1000, 1000]
)
),
New Column( "X__4",
Numeric,
"Continuous",
Format( "Best", 12 ),
Set Values(
[165.784, 185.631, 182.692, 321.191, 222.253, 190.369, 141.291, 238.045, 155.8, 193.864, 211.71, 169.878, 248.122, 343.904, 219.022,
213.807, 234.497, 228.624, 221.81, 303.131, 233.672, 240.283, 262.04, 234.113, 230.559, 302.435, 234.924, 180.417, 204.864, 192.121,
208.654, 279.997, 221.742, 253.428, 333.66, 228.471, 228.203, 306.936, 195.709, 179.987, 198.901, 182.383, 174.387, 190.804, 202.056,
251.821, 162.966, 151.297, 227.295, 243.323, 308.69, 250.501, 178.237, 205.268, 186.931, 264.835, 253.206, 180.248, 228.354, 173.267,
209.035, 316.253, 233.827, 261.515, 436.17, 304.096, 198.555, 192.5, 174.545, 216.619, 263.621, 224.102, 165.699, 172.02, 184.339,
319.142, 273.346, 241.685, 250.863, 279.174, 282.074, 234.905, 271.268, 246.504, 234.255, 234.621, 215.857, 198.827, 178.571, 253.006,
165.905, 176.766, 165.9, 156.998, 174.871, 138.317, 158.778, 168.471, 177.843, 156.39, 164.241, 181.16, 211.527, 166.767, 183.864,
174.666, 208.884, 184.8, 242.95, 258.45, 266.48, 223.222, 238.027, 251.496, 188.257, 217.88, 223.415, 142.726, 202.957, 189.208, 233.86,
172.37, 156.7, 166.967, 194.361, 136.632, 177.214, 189.665, 168.163, 123.795, 124.455, 121.122, 141.333, 140.665, 123.588, 177.002,
205.106, 170.312, 165.658, 172.969, 139.313, 159.358, 186.585, 124.064, 119.142, 159.607, 126.957, 172.168, 191.619, 155.268, 124.592,
179.188, 143.001, 136.861, 134.006, 135.829, 182.537, 247.613, 169.255, 155.949, 206.608, 142.226, 163.47, 149.018, 136.844, 153.43,
233.462, 157.986, 183.982, 228.304, 152.392, 153.049, 129.58, 145.692, 168.966, 209.656, 157.609, 157.981, 125.511, 121.536, 139.82,
151.759, 130.494, 150.392, 219.372, 177.769, 167.091, 226.695, 156.332, 178.79, 157.629, 155.362, 196.008, 148.454, 155.809, 156.316,
201.067, 177.872, 143.322, 159.838, 142.441, 159.66, 175.081, 153.589, 150.38, 211.264, 128.639, 161.971, 239.547, 156.63, 199.718,
215.102, 255.392, 135.287, 214.074, 174.491, 316.539, 212.039, 193.07, 230.615, 272.108, 265.911, 242.919, 275.754, 226.606, 185.626,
207.183, 107.479, 181.01, 160.927, 154.999, 212.347, 207.103, 206.981, 173.252, 162.523, 145.3, 209.405, 238.121, 201.926, 140.379,
169.733, 140.031, 190, 210.817, 182.863, 154.491, 141.725, 148.018, 126.14, 129.716, 115.108, 230.213, 221.9, 175.315, 144.772, 138.977,
126.068, 123.83, 137.769, 117.228, 129.679, 173.974, 150.659, 168.899, 234.318, 172.725, 178.6, 134.249, 120.719, 122.413, 150.555,
129.722]
)
)
)Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Understanding Statistical Details for Variance Components
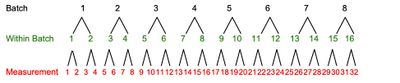
Nested "layers" mean that subordinate layers are dependent upon the layer above it (every value is unique). These are also called hierarchical. A simple example is in a batch manufacturing process, samples taken from within batch are nested in batches. The sampling tree might look like this:
Note that each layer has a sequential numbering scheme.
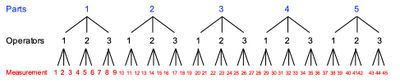
Crossed studies have no hierarchy. Crossed studies allow for the estimation of interactions between layers (e.g., typical factorial designs are crossed studies). They are called crossed because an interaction plot will depict lines as crossed (if they are parallel, there is no interaction). The numbering scheme is how this is "communicated" to the software (e.g., repeated pattern in the numbering). Of course, these conditions can be combined in the same plan. The following is an example where the top two layers are crossed and the bottom layer is nested:
In this plan every operator sees every part.
There are also plans with systematic sampling, but that is for another discussion.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Understanding Statistical Details for Variance Components
If you want details, check out the 2015 JMP Discovery paper by @Laura_Lancaster. More generally, I'm sure the Mastering JMP session by @JerryFish would be of interest.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Understanding Statistical Details for Variance Components
To add to my (I'm now retired,,,) former colleague @ian_jmp 's sound advice I'll add a few thoughts.
1. One way I've found to help determine the nesting and crossing within an experiment...because that's where these properties are determined is to make a tree diagram not unlike the variability chart display or shown in the Mastering JMP event @ian_jmp and then ask yourself, does this effect (part, operator, etc.) stay within a branch and if so where, or does it cross over higher level factors within the tree structure. So an example might be the parts. If each operator is measuring the SAME parts, then some amount of crossing for the parts is called for. But let's say the devices being used by each operator are unique to that set of operators, then the devices are nested within the operators.
2. Another thought is decide on the specific computational method used for calculating variance components. Historically, EMS (an acronym for Expected Mean Square) was used...one shortcoming here is potential negative variance estimates...which don't make sense...but people still use it and JMP still supports it...but most nowadays use another method such as REML (which is an acronym for REstricted Maximum Likelihood. JMP supports this as well.
3. Last thought is how all the factors have to be defined as either 'fixed' or 'random' effects within the model. An example of a fixed effect would be your operators are 'fixed' if they are the entire population of operators that will ever, in perpetuity, work in the system. What are those chances? Probably zero. But hopefully you get the point. An example of a 'random' effect could be the parts used in the experiment. If the parts are a randomly selected collection of parts from some larger population of potential parts that could have been included in the experiment then they would be a 'random' effect.
I'm sure I'm leaving something out...hopefully others will chime in.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Understanding Statistical Details for Variance Components
Nested "layers" mean that subordinate layers are dependent upon the layer above it (every value is unique). These are also called hierarchical. A simple example is in a batch manufacturing process, samples taken from within batch are nested in batches. The sampling tree might look like this:
Note that each layer has a sequential numbering scheme.
Crossed studies have no hierarchy. Crossed studies allow for the estimation of interactions between layers (e.g., typical factorial designs are crossed studies). They are called crossed because an interaction plot will depict lines as crossed (if they are parallel, there is no interaction). The numbering scheme is how this is "communicated" to the software (e.g., repeated pattern in the numbering). Of course, these conditions can be combined in the same plan. The following is an example where the top two layers are crossed and the bottom layer is nested:
In this plan every operator sees every part.
There are also plans with systematic sampling, but that is for another discussion.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Understanding Statistical Details for Variance Components
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Understanding Statistical Details for Variance Components
Thank you @ian_jmp , @P_Bartell , and @statman for the excellent input. Much appreciated.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us