- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Trend Evaluation where X = Ordinal and Y = Continuous?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Trend Evaluation where X = Ordinal and Y = Continuous?
Hi JMP Community,
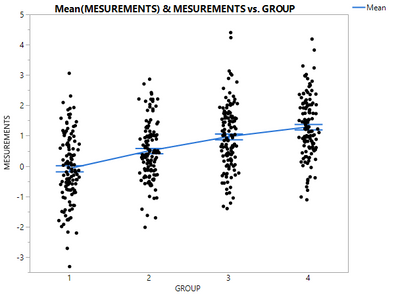
I would like to know if it is possible to evaluate(in JMP 13.1) trends in a data where X is ordinal (4 Groups) and Y is continuous (see attached file).
Based on a visual inspection, it appears that the means of Measurements are progressively higher with each group but I have not been able to find a method to evaluate this formally.
Thank you for your help.
TS
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Trend Evaluation where X = Ordinal and Y = Continuous?
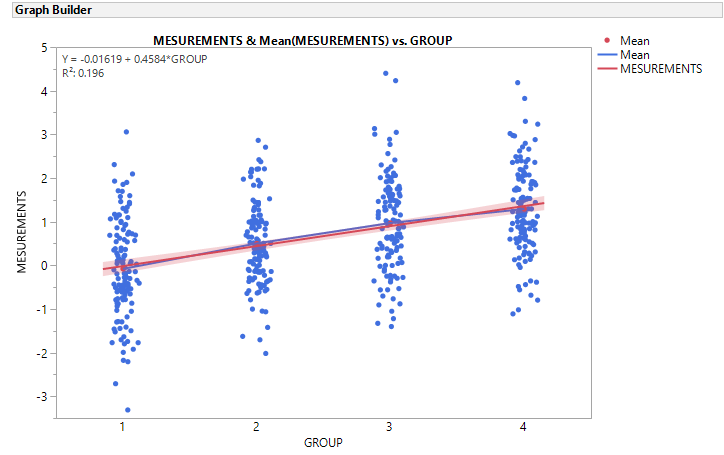
@Thierry_S, in JMP 13 Graph Builder, you can add a Line of Fit via the UI or use this saved script
Graph Builder(
Variables( X( :GROUP ), Y( :MESUREMENTS ) ),
Elements(
Points( X, Y, Legend( 3 ) ),
Points( X, Y, Legend( 4 ), Summary Statistic( "Mean" ) ),
Line( X, Y, Legend( 5 ) ),
Line Of Fit( X, Y, Legend( 6 ), R²( 1 ), Equation( 1 ) )
),
SendToReport( Dispatch( {"Line Of Fit"}, "", OutlineBox, {Close( 0 )} ) )
)Here is the result.
However, I would follow this approach:
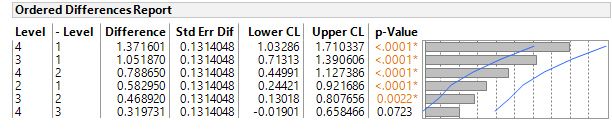
- Use Analyze > Fit Y by X to run a one way ANOVA, the means should increase with Group and you should test for global significance difference in the means then compare the groups. For example, does Group 3 have a statistically different mean that Group 4, etc.
- Look at the successive differences in the group means ( 2-1, 3-2, 4-3), they are are all positive (0.58, 0.47, 0.32). 4-3 is not significant at 0.05, however, the p-value is 0.07 which provides some indication of a trend, but maybe slowing.
- I would not recommend a higher order model without more context on this ordinal Group. For example, this could be the luck of the draw, that the order of these four groups result is 1,2,3,4 one out of 24 possible ordering (4! different outcomes). If there is a "cause" for this ordering like dose, or repetition (learning) or some social group, the model should be built using the "cause" variables.
- A simple method other than Graph Builder to support the "trend" is to right click on the means and standard deviation table and select Make into Data Table. Then use Fit Y by X with the Mean as Y and Group as X (make it continuous) the ft the line
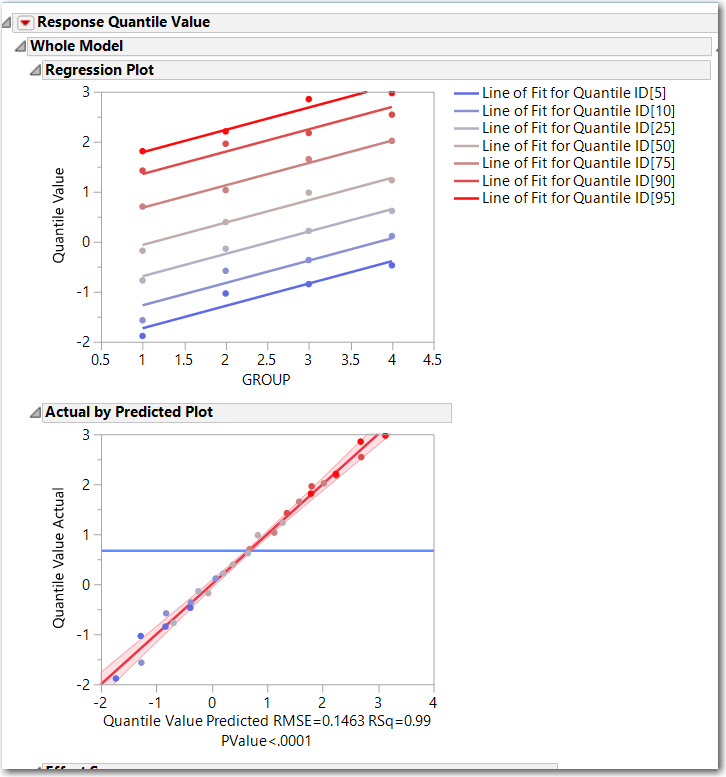
However, when looking for a shift in the "distribution" of these groups, I like to take a different approach:
- From your table, compute the distribution quantiles for each Group, 95, 90, 75, 50, 25, 10, 5 using Tables > Summary. The resulting table needs a little work: stack the quantiles, simplify the Quantile ID.
- Then I like to look at the relationship of the 90th percentile (for example) across the groups. Is it changing as much of as the mean?
- The summary QuantizedTable and the script to create the analysis below is attached to the table. This graphic indicates that the entire distribution is shifting, not just the mean... which lends strength to the argument of a trend by group
Let me reiterate, this is an exploratory analysis. Any modeling or further investigation should be placed on the drivers/cause of the shift.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Trend Evaluation where X = Ordinal and Y = Continuous?
@Thierry_S, in JMP 13 Graph Builder, you can add a Line of Fit via the UI or use this saved script
Graph Builder(
Variables( X( :GROUP ), Y( :MESUREMENTS ) ),
Elements(
Points( X, Y, Legend( 3 ) ),
Points( X, Y, Legend( 4 ), Summary Statistic( "Mean" ) ),
Line( X, Y, Legend( 5 ) ),
Line Of Fit( X, Y, Legend( 6 ), R²( 1 ), Equation( 1 ) )
),
SendToReport( Dispatch( {"Line Of Fit"}, "", OutlineBox, {Close( 0 )} ) )
)Here is the result.

However, I would follow this approach:
- Use Analyze > Fit Y by X to run a one way ANOVA, the means should increase with Group and you should test for global significance difference in the means then compare the groups. For example, does Group 3 have a statistically different mean that Group 4, etc.
- Look at the successive differences in the group means ( 2-1, 3-2, 4-3), they are are all positive (0.58, 0.47, 0.32). 4-3 is not significant at 0.05, however, the p-value is 0.07 which provides some indication of a trend, but maybe slowing.
- I would not recommend a higher order model without more context on this ordinal Group. For example, this could be the luck of the draw, that the order of these four groups result is 1,2,3,4 one out of 24 possible ordering (4! different outcomes). If there is a "cause" for this ordering like dose, or repetition (learning) or some social group, the model should be built using the "cause" variables.
- A simple method other than Graph Builder to support the "trend" is to right click on the means and standard deviation table and select Make into Data Table. Then use Fit Y by X with the Mean as Y and Group as X (make it continuous) the ft the line
However, when looking for a shift in the "distribution" of these groups, I like to take a different approach:
- From your table, compute the distribution quantiles for each Group, 95, 90, 75, 50, 25, 10, 5 using Tables > Summary. The resulting table needs a little work: stack the quantiles, simplify the Quantile ID.
- Then I like to look at the relationship of the 90th percentile (for example) across the groups. Is it changing as much of as the mean?
- The summary QuantizedTable and the script to create the analysis below is attached to the table. This graphic indicates that the entire distribution is shifting, not just the mean... which lends strength to the argument of a trend by group
Let me reiterate, this is an exploratory analysis. Any modeling or further investigation should be placed on the drivers/cause of the shift.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us