- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Survival Statistics: Cage mortality
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Survival Statistics: Cage mortality
Hello,
Firstly I would like to thank the community for being here to help with newbe questions. Ever since moving to this institution I have loved JMP!
I am trying to do survival statistics for a study where I tracked cage mortality for 18 cages containing 50 flies each across 20 days. The cages each have variable number of dead per day. After reading and watching the "Advanced Mastering JMP: Analyzing Survival Data " I am still at a loss and wondering if this survival analysis is not suited for my type of stats. Maybe I would be better suited with a regression or something.
Any suggestions or tips on better sources for troubleshooting would be greatly apreciated.
Joe
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Survival Statistics: Cage mortality
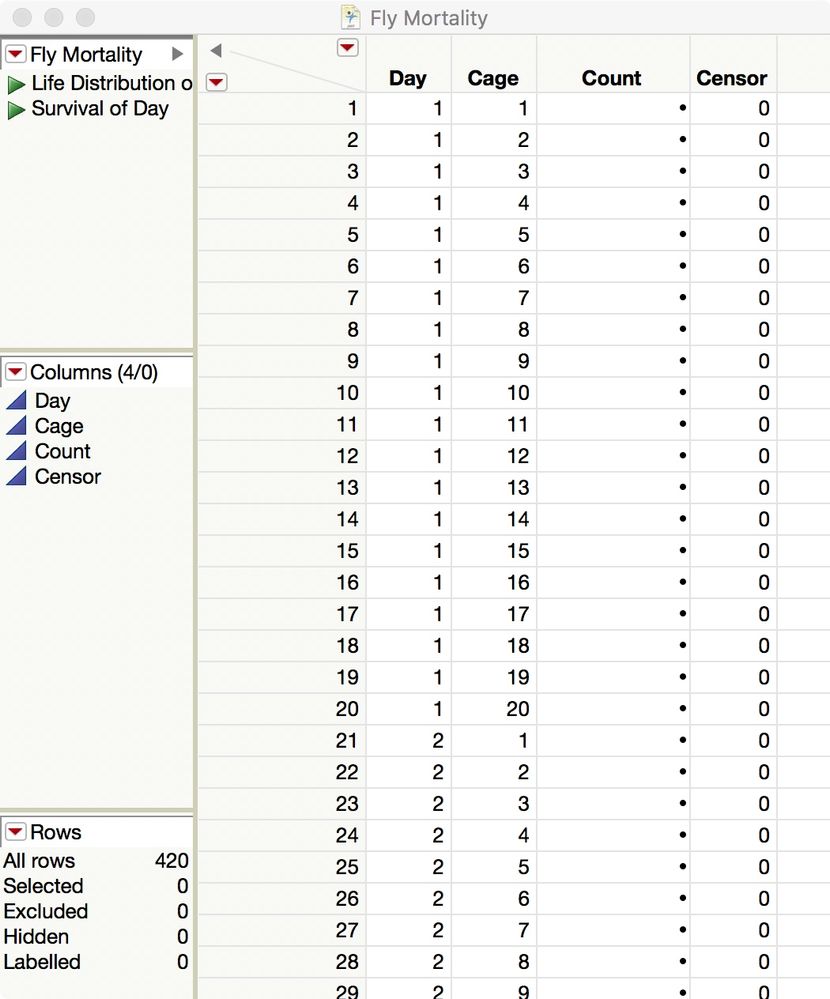
I think that there are at least three ways to analyze the mortality in JMP: Life Distribution, Survival, and Probit (using GLM in Fit Model). Let's start with the first two. You data is fine but it should be organized like this:
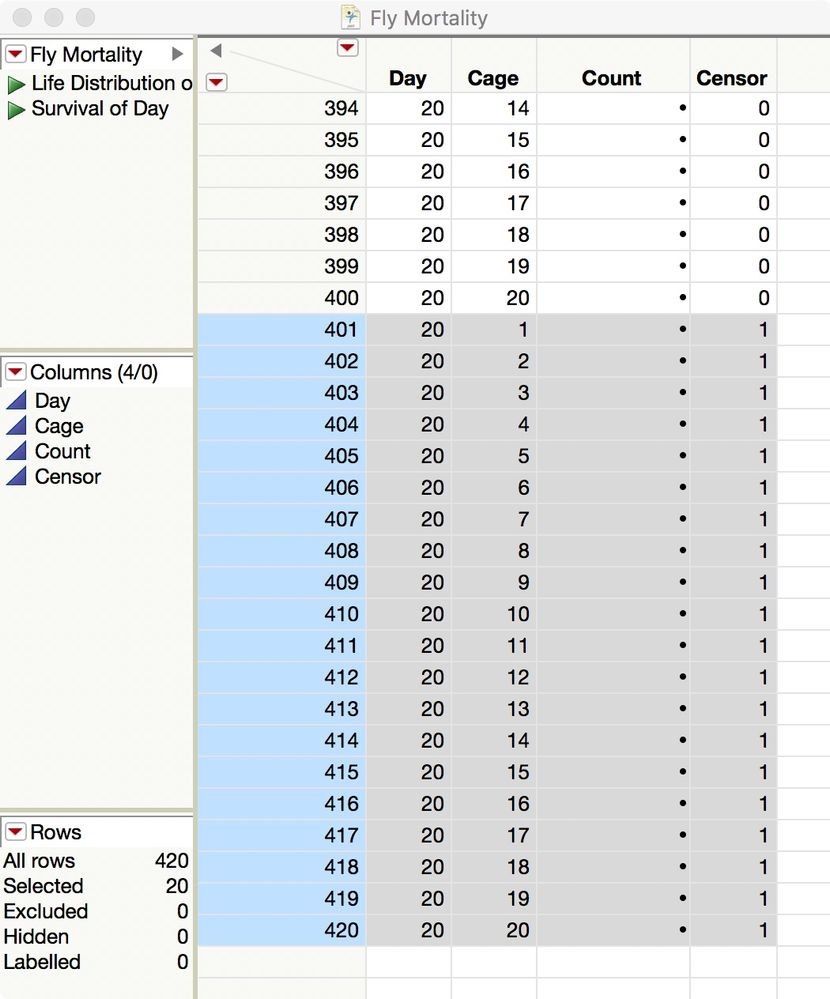
You have 20 cages running for 20 days. Enter the number of new dead flies in the Count column for a given day and cage. Enter the number of surviving flies at the end of the table, in the rows with Censor = 1:
Then use the two saved table scripts to start the analyses.
I attached this template data table for you so you have to do is enter the Count data.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Survival Statistics: Cage mortality
Survival analysis is suitable here (but it does not exclude other methods - it depends on your aims). So, in the data table you have the colums:
1. number of fly (1, 2, 3 etc)
2. died (1), alive (0, this is censor cod). (Note, in JMP by default censor code is 1, so you need to change it)
3. time to death (if the fly died) or 20 days (if the fly is alive)
4. cage code (if it matters to you)
P.S. If you turn curve ie. that the curve goes from bottom to top (the survival platform gives you this possibility), you will get a cumulative probability of death
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Survival Statistics: Cage mortality
Right now I have the data recorded as mortality per day per cage. The cages are the replicates and I am not concerned with individual flies, but rather the overall survival of each cage population. The method you mention above would have me catalog the survival of 900 individual flies. This would take a tremendous amount of time! Not to mention I have data from a repeat study with the same amount of replicates.
My data is merely the tracking of loss over 20 days for each cage. I was hoping there would be an easier way to do this in JMP.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Survival Statistics: Cage mortality
And if some fly flies before 20 days you will need to put her not 20 days, but the day of her flight (these are the rules of censoring). P.S. With flies you need to be careful, especially if consider, who is called the prince of flies ... :)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Survival Statistics: Cage mortality
OK. 1. On the 20th day, open the cage and see how many flies are alive (a), and how many died (d). Such for each cell.
2. You will get a series of numbers
a1, d1 (for first cage)
a2, d2 (for second)
a3, d3 (for third)
etc.
3) Then do a pair comparison with contingency tables 2x2 ("Fit Y by X" platform)
Compare:
a1, d1
a2, d2
then сompare:
a1, d1
a3, d3
then сompare
a2, d2
a3, d3
etc.
4) As a result, you can select the cage pairs that are statistically significantly different (exact Fisher test). I don't think there will be many of them.
P.S. If the cage are independent, then the effect of multiple comparisons will not be.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Survival Statistics: Cage mortality
I think that there are at least three ways to analyze the mortality in JMP: Life Distribution, Survival, and Probit (using GLM in Fit Model). Let's start with the first two. You data is fine but it should be organized like this:
You have 20 cages running for 20 days. Enter the number of new dead flies in the Count column for a given day and cage. Enter the number of surviving flies at the end of the table, in the rows with Censor = 1:
Then use the two saved table scripts to start the analyses.
I attached this template data table for you so you have to do is enter the Count data.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Survival Statistics: Cage mortality
Thank you kindly
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Survival Statistics: Cage mortality
Hi markbailey: Could you please provide added info on how to cast selected columns into roles? I've transformed my dataset as recomended, but also have 2 treatments and wonder if I'm entering the data right. So I have "phase" as Y, Time to Event; "Censor" column as Censor; "Count" column as Freq; and wonder if "Treatment" should be entered as By. The problem with this structure is that i fdont get a comparison between treatments. Can you please help?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Survival Statistics: Cage mortality
I have not looked at this problem in a long time. Let's start over and make sure that the solution suits your situation. Does this brief description capture your case?
- You divide cages over two treatments A and B.
- You have c cages and half of them go to each treatment.
- You have n subjects in each each cage at the start.
- You observe the number of subjects alive/dead each day for d days.
I do not know your standard analysis for such a case but there are three general approaches that I can think of, which seem suitable. You could perform a probit analysis using a Generalized Linear Model with a Poisson distribution and a probit link function. Treatment would be the only fixed effect. You could also perform a parametric survival analysis if you have a distribution model in mind. You could also perform a proportional hazards analysis without specifying the hazard function if the assumption is valid.
If this description seems appropriate, then I can help you with the layout of your data table and the set up of the analysis.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Survival Statistics: Cage mortality
Yes, your description fits my dataset, just that I have phases (4) rather than days. Mortality is low (~5% of the entire dataset), and so it does not have normal distribution. I transformed the dataset to mimic the Fly Mortality example and ran Fit Life by X analysis. It confuses me that it shows a Wilcoxon Group Homogeneity Test (Chi-Square), as well as “No Effect vs. Location” (effect different from zero?), and a “Location vs. Location and Scale”. So I’m not sure whether one of those reflects the 2 treatment comparison.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us