- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- capability analysis using control chart builder
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
capability analysis using control chart builder
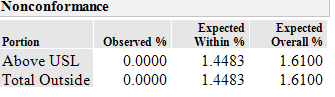
I got machine in lab for which I have set limits and I am trying to find out what is the probability of failing in the the future or if I'll get readings out of spec. First I used control chart builder and then did capability analysis and I got the following nonconformance table. Is this telling me that 2 out of 100 reading will be out of spec? What is expected within %?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: capability analysis using control chart builder
See the excerpt below, from the JMP Help select Scripting Index > Objects > search for nonconformance then press the Topic Help button.
Overall Sigma will be larger than Within Sigma, and % out of spec will be larger. If your data is representative of the full population and can be modeled as a normal distribution and your specified control chart subgrouping, then yes 16 out of 1000.
JMP Help:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: capability analysis using control chart builder
See the excerpt below, from the JMP Help select Scripting Index > Objects > search for nonconformance then press the Topic Help button.
Overall Sigma will be larger than Within Sigma, and % out of spec will be larger. If your data is representative of the full population and can be modeled as a normal distribution and your specified control chart subgrouping, then yes 16 out of 1000.
JMP Help:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: capability analysis using control chart builder
Thank you gzmorgan0 for the explanation.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us