- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Survival Statistics: Cage mortality
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Survival Statistics: Cage mortality
Hello,
Firstly I would like to thank the community for being here to help with newbe questions. Ever since moving to this institution I have loved JMP!
I am trying to do survival statistics for a study where I tracked cage mortality for 18 cages containing 50 flies each across 20 days. The cages each have variable number of dead per day. After reading and watching the "Advanced Mastering JMP: Analyzing Survival Data " I am still at a loss and wondering if this survival analysis is not suited for my type of stats. Maybe I would be better suited with a regression or something.
Any suggestions or tips on better sources for troubleshooting would be greatly apreciated.
Joe
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Survival Statistics: Cage mortality
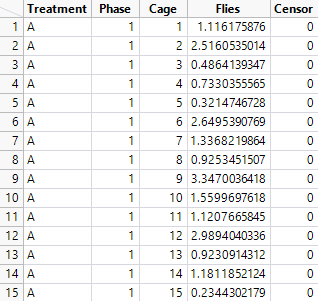
I mocked up your study:
Treatment is A or B. Phase is 1 to 4. Cage is 1 to 20. Flies is the count of dead flies. Censor is set to 0 for dead. The rows for Phase = 4 are duplicated to record the number of flies still alive and Censor is set to 1 for those rows.
Note that Flies is a random number from a Weibull distribution so I could continue my reply.
The homogeneity test assumes a null hypothesis that the distribution of all the groups (Treatment in this case) are the same. The alternative hypothesis is that the distributions are not all the same. This is the test for any Treatment effect.
The Nested Models Tests are also for a Treatment effect, but they address the nature of the Treatment effect. These tests also start with the assumption of no effect. The first test compares the location parameter. The second compares the location and the scale parameter.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Survival Statistics: Cage mortality
Thank you so much!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Survival Statistics: Cage mortality
It seems to me that in this research there is no interest in the dynamics of the process, but are interested in comparing the types of replications by final (on the 20th day) results (ratio of dead and live in percent), i.e. want to find a statistically significant difference in the proportions of live and dead depending on replication (cages)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Survival Statistics: Cage mortality
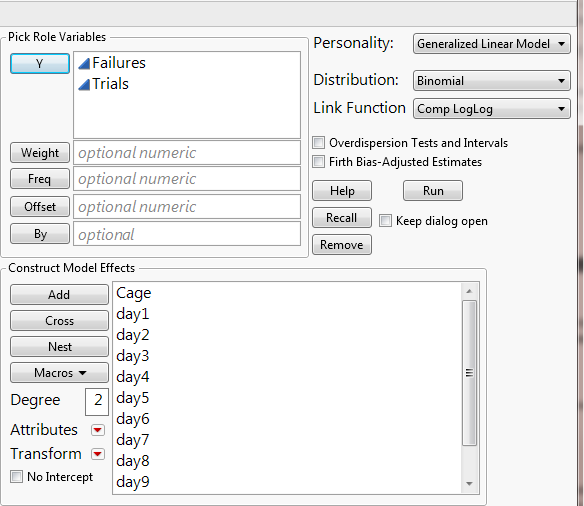
I wanted to introduce a so-called “Complementary Log-Log model” for binomial response data as you have (i.e., # of dead files per cage population). This model is often applied to discrete survival time data.
The model is available in Fit Model’s Generalized Linear Model personality by choosing Distribution: Binomial and Link Function: Comp LogLog.
Suppose you have recorded mortality (# of failures) for each cage at the end of Day 20. Let N be the cage population (i.e., trials). You will add both the mortality count and N columns as Y, and add Cage and any other covariates as model effects. The results allow you to test if the overall mortality rates differ significantly by cage and to predict the mortality.
If you want to estimate the baseline survival function then you would need to create a series of indicator variables that identify # of dead flies for each day and add them as model effects.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Survival Statistics: Cage mortality
Please, specify for JMP 10.
Analyze=>Fit model=>?
I don't see "Generalized Linear Model" here. Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Survival Statistics: Cage mortality
Please also check out this JMP blog post https://community.jmp.com/t5/JMP-Blog/Reliability-regression-with-binary-response-data-probit-analys...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Survival Statistics: Cage mortality
Select Analyze > Fit Model. Then click the button next to Personality and select Generalized Linear Models near the bottom of the drop down menu. You should see the choice for distribution and link function appear after that
I still think that your biggest hurdle is the layout of your data table. It isn't difficult, but if you don't set up the data correctly you will have trouble with most of the procedures. Did you try the layout I suggested?
A different layout is necessary for the GLM approach...
- « Previous
-
- 1
- 2
- Next »
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us