- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Split plot DoE (limiting number of trial runs per day)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Split plot DoE (limiting number of trial runs per day)
Hello everyone,
New case:
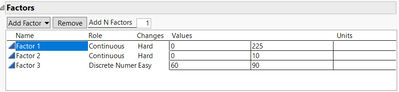
3 variables (factors)
Factor 1 (Continuous) = 0 - 225
Factor 2 (Continuous) = 0 - 10
Factor 3 (Discrete - 2 level) = 60 and 90 (process step)
Factor 3 can be considered as a final processing step for the mixture of the first 2 factors. So as an example:
Factor 1 (225) combined with Factor 2 (10) - this batch would ideally be treated both at 60 and 90 the same day.
The limiting/challenging part is the number of batches that can be done pr. day. There is only time to mix 2 batches per day with a 8 days of trial in total. Meaning up to 16 batches and "32 unique runs".
I have tried different solutions with blocking/hard to change factors. However the power analysis comes out quite poor if I set both continuous factors as hard to change.
I am interested in a model that can explain the following:
The 3 main factors
All interaction terms
Factor 1 X Factor 1
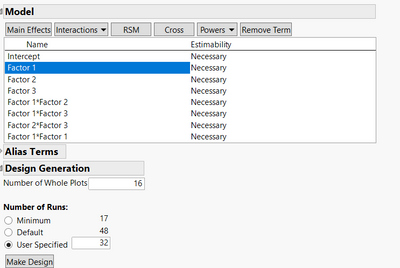
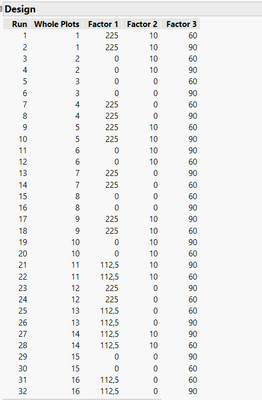
My current setup can be seen in the pictures attached.
There might be several some solution I have not considered. Could really use some inputs.
Looking forward to your response. Currently using JMP 17 - not capable of writing/working with JSL scripting.
Technology Specialist
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Split plot DoE (limiting number of trial runs per day)
Hi Kristian,
One possible option is to consider the two factors 1 and 2 as "Hard to change", and factor 3 as "Easy to change" :
Then, create your model with main effects, interactions and quadratic power for factor 1. Specify the number of Whole plot to 16 and the number of runs to 32 :
You'll have 2 runs per whole plot (for a total of 2 batches/4runs per day, so 2 whole plot per day) in which only the factor 3 will vary :
You can find the datatable for the design attached to evaluate the design and see if it fits your needs.
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Split plot DoE (limiting number of trial runs per day)
Hi Kristian,
One possible option is to consider the two factors 1 and 2 as "Hard to change", and factor 3 as "Easy to change" :
Then, create your model with main effects, interactions and quadratic power for factor 1. Specify the number of Whole plot to 16 and the number of runs to 32 :
You'll have 2 runs per whole plot (for a total of 2 batches/4runs per day, so 2 whole plot per day) in which only the factor 3 will vary :
You can find the datatable for the design attached to evaluate the design and see if it fits your needs.
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Split plot DoE (limiting number of trial runs per day)
Hi @Bertelsen92 ,
@Victor_G 's solution makes sense to me and it seems to meet your requirements.
In your example you had specified 7 whole plots and 26 runs total, which would be strange.
The number of whole plots is the number of groups of runs within which the hard-to-change factors remain constant. Hence, Victor set this to 16 because you can execute 2 combinations of your hard-to-change factors each day, over 8 days, 32 runs total.
You were worried about the power. The power will be lower when you set factors as hard-to-change. In designed experiments we learn about the effect of a factor on the response by changing the factor and observing the effect on the response. If we make fewer changes to the factor, we learn less. It is no more complicated than that.
Having said this, the absolute number that you see for power is only meaningful if you have good numbers for the noise (RMSE) and signal you need to detect (anticipated coefficient). Most times we don't have these. So if you are just using the JMP defaults (RMSE = 1, coefficient = 1), there is no sense in worrying about whether the power is > or < 0.8.
I hope this helps.
Phil
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Split plot DoE (limiting number of trial runs per day)
Hi @Phil_Kay,
Thanks for the support and explanations provided for the design proposed.
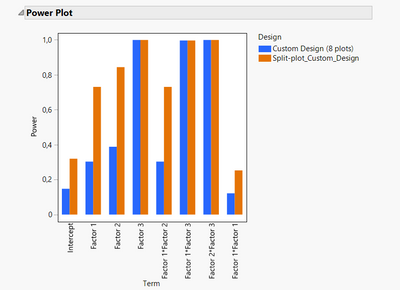
In its original design, Kristian defined 7 plots and 28 runs, in order to respect and realize the 4 runs/day condition. It could have been possible, since the highest possible number of runs is 32, to also use 8 plots and 32 runs to realize the 4 runs/day condition.
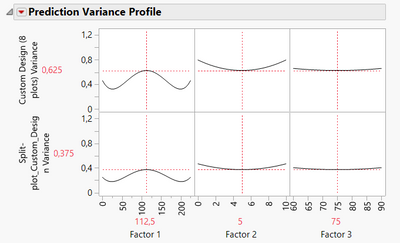
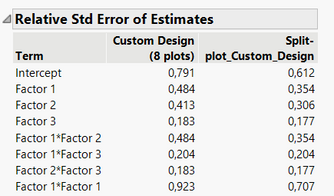
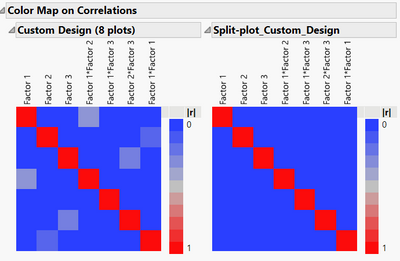
But if doing this design, that means the runs in each plot will be similar for the "hard-to-change" factors, so there will be 4 identical batches per day, at 2 conditions for the factor 3. This situation may not impact the power (comparatively to the design I have proposed earlier) for factor 3 since there is a randomization possible for factor 3 in each block (easy to change factor), but due to the "hard to change factors" which imply a severe restriction on randomization for these factors, it will affect the power of the "hard-to-change" factors 1 and 2, as well as the prediction variance for these 2 factors, precision of these parameters estimates, and aliases in the design :
Comparison of power between designs with 8 plots and 16 plots:
Comparison of prediction variance between designs with 8 plots and 16 plots:
Comparison of relative standard error of estimates between designs with 8 plots and 16 plots:
Comparison of correlations between terms in the model for both designs :
I hope this answer will help and complement the great explanations of Phil,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Split plot DoE (limiting number of trial runs per day)
Makes sense, @Victor_G . Sorry, I had misread the 28 runs as 26. In any case, your 16 whole plot design will clearly be "better" than 7 or 8 whole plots. The relative difference in power is a useful indicator here: more changes to the factors => more power. But, again, I would stress that the absolute value of power is meaningless unless you have meaningful numbers for the size of the noise and the signal you need to detect.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Split plot DoE (limiting number of trial runs per day)
Thank you so much for all your input Victor and @Phil_Kay. Really good explanation and solution to the case I proposed.
I think I might have overestimated the importance of the "power score" since I do only use the JMP default (RMSE = 1, coefficient = 1).
I will go with your solution with the 32 runs and 16 plots. Really good with the comparison feature of the two designs, will definitely try that out next time myself.
Have a nice weekend both.
Technology Specialist
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Split plot DoE (limiting number of trial runs per day)
Hi @Victor_G and @Phil_Kay ,
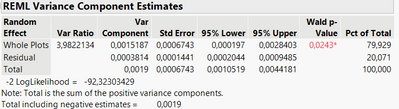
The trial has now been conducted, and I am looking into the Fit model platform for several responses measured. I have one question regarding the WholePlot*Random effect.
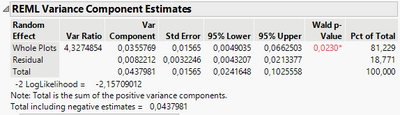
So for one of the responses, I get the following:
So the Whole Plots (Pct of total = 81,229). It is correctly understood that 81% of the variance of this data cannot be explained by the factors we have changed, but is more likely to come from something else. In this case, it does make really good sense. Just wanted to make sure I understood it correctly.
Secondly, does it then make sense to use the Prediction Profiler if only 18% of the data is "valid"?
Thank you in advance. Have a great weekend. :)
Technology Specialist
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Split plot DoE (limiting number of trial runs per day)
Hi @Bertelsen92,
I think you'll find the explanation from @Mark_Bailey very useful regarding the differences between random and fixed effects : Solved: Re: meaning of random effects p-value in the report - JMP User Community
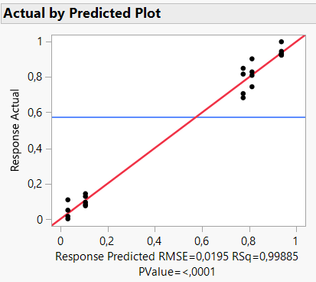
In your case, 81% of the variance can be imputed to your random effect, your day variable. Having a significant Wald p-value means that the response variance depends on the random effect, so your day variable (the whole plot). But that doesn't mean that your data is "rubbish". You can also first visualize your data and/or your model through different platforms, for example looking at the "Actual by Predicted Plot" available in different modeling platforms might already tell you if you can get a sensible model for your data or not (example from my sample datatable to reproduce the same conditions you have):
As an example, I added non-constant noise (increasing with the number of the row), and I have a very similar display like you for REML :
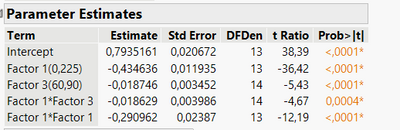
But looking at the fixed effect estimates (and after removing non-significant effects), I was able to detect 2 significant main effects, 1 significant interaction and 1 significant quadratic effect :
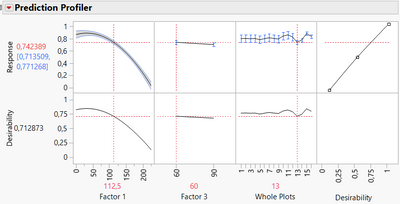
Depending on how large is your noise/variance (compared to the difference between levels' means you want to detect for the different factors/effects), your predictive performance might not be high. But it's worth to look at the Profiler, to have a feeling about how each factors may affect the response.
Additional option for the Profiler: In the red triangle, you can click on "Conditional Predictions" in order to see the model's predictions by fixing the random effects: Prediction Profiler Options (jmp.com) This might be helpful if you want to have a look on the model and the factors' effects by controlling the variance from the random effect.
Example here on the sample data :
I added my example shown here so that you can reproduce the results I have shown by looking at the script "Model final".
I hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Split plot DoE (limiting number of trial runs per day)
Hi,
The REML Variance Component Estimates part of the report is telling you about the amount of error variance that is captured by the random (whole plot) effect versus the residual error. It is incorrect to interpret it as 18% of the data is "valid". You should interpret it as 18% (or actually 19%) of the error variance is not accounted for by the whole plot effect.
I hope this helps,
Phil
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Split plot DoE (limiting number of trial runs per day)
Sorry, I can't help myself. I look at the problem slightly differently...You have a huge opportunity to improve your process by understanding what is actually changing day-to-day. Why does the process change so much day-to-day? Do the factor effects stay consistent day-to-day or do they vary?I'm too deterministic to believe that random variation can't be understood, explained and likely modeled with the right effort. This does require some persistent and diligent work to identify variables that change day-to-day and determine your ability to manage those variables in the long-term and if you can't, how to develop a process that is robust to those variables. Having a model that "predicts" the mean without understanding what causes variation is a bit like this old phrase:
"Feet in the oven, head in the freezer, on average the perfect temperature"
BTW, your small screen shot does not tell us some important information in determining the model adequacy (e.g., RSquares, RMSE, Residuals analysis). Also, those %'s apply only to the data in hand and do not necessarily mean you will get the same results in the future.
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us