Structural equation models: how to handle confounding variables

[#1]

As someone new to SAS JMP structural equation modeling (SEM), I am seeking advice on how to properly address confounding variables in my SEM analyses.  I could not find appropriate guidelines about how control for these confounding variables in the current literature. 

 I would appreciate any suggestions that can ensure that confounding variables are properly accounted for. Thank you in advance!

[#2]

Hi @Hcrooo,

Perhaps the easiest way to think about properly addressing confounding variables in SEM is by using a linear regression example. Suppose we're interested in examining the effect of body-mass index (BMI) on blood pressure (BP). Using the "Diabetes.jmp" sample data table, I can fit a simple linear regression in SEM and the results would look like this,

suggesting that one unit increase in BMI results in a 1.24 unit increase in BP. However, we're concerned about age as a confounder, so we want to add it to the model to properly adjust for its effect. We would do this by adding age as predictor of BP, and also by adding its covariance with BMI. The results would look like this,

 

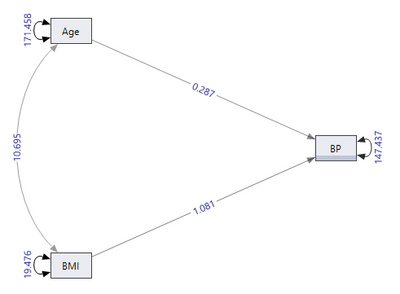
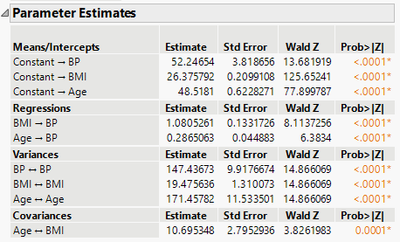
We can see that all the effects are statistically significant and the effect of BMI on BP is now smaller (1.08) because we're controlling for age. Your SEM application might be more complex than this example, but the general idea is that the confounder should be added as a predictor into the equations where you want to adjust for it, and the confounder's associations with other variables in the model should also be specified (in this case we added the covariance with BMI).

HTH,

~Laura