Samples required to determine Normal Distribution Plot

[#1]

Dear JMP,

May I know is there a minimum number of samples that is required before we can actually use to determine whether the sampes that we have falls under the normal distribution category. 

I have a sample of 10 datas is this sufficient to show whether all these data falls under the normal distribution category

Rgrds

Irfan

[#2]

The minimum sample size to fit a normal distribution model (estimate mean and standard deviation) and perform the Shapiro-Wilk hypothesis test (H0: population is normal versus H1: population is not normal) is 2.

What do you mean by "actually use to determine?"

Your question might be about the power of the test to reject the null hypothesis. There is little power in the minimum sample size 2. Many experts, including JMP, consider the issue moot, though. By the time you have sufficient sample size to test normality with reasonably high power, the normality assumption of most popular statistics or tests will be met due to the central limit theorem (the sum of random variables is normally distributed as the sample size increases toward infinity).

For example, a critical assumption of the one sample t-test is that the sample mean is normally distributed. If the population of data is normally distributed, then the sample mean is normally distributed. So we test the normality of the sample to decide about the normality of the population. What if the sample fails this test for normality? What if the population is not normal? Well, it might be a problem or it might not. It depends on the skewness of the population.

Remember that the assumption is about the distribution of the sample mean. A normal population (of data) is only one way that you might obtain normally distributed sample means. The sample mean is computed as the (weighted) sum of the observations, that is, random variables. Therefore, these sample means will be sufficiently normal, regardless of the distribution of the population, if the sample size is large enough and so the assumption of the t-test will be valid. Again, it depends on the population distribution skewness.

You can compute the minimum sample size for nomality under the CLT from the estimate of the skewness or you can use a rule of thumb. (One popular rule is a sample size of at least 30 is sufficient.)

In the end, it comes down to using the sample that you have to determine normality.

Why are you deciding if the population is normal? What is the normality assumption for?

[#3]

Hi Mark,

Thanks, what I am looking for is that I have a set 9 data as shown below. From the rough estimates i can see that there is two population of data which is  ~ 2.3 and ~ 2.2. I would like to find out whether the 2.2 actually belongs to the same normal population as the 2.3. In other words whether the 2.2 data actually falls with the same population as the rest of the data.

2.26
2.23
2.43
2.33
2.36
2.36
2.35
2.32
2.23

What kind of analysis can I do to determine this?Is the normal quantile plot and shapiro wilk test is sufficient

[#4]

What did you use for your "rough estimate?" Why do you think that there are two populations in this sample of data?

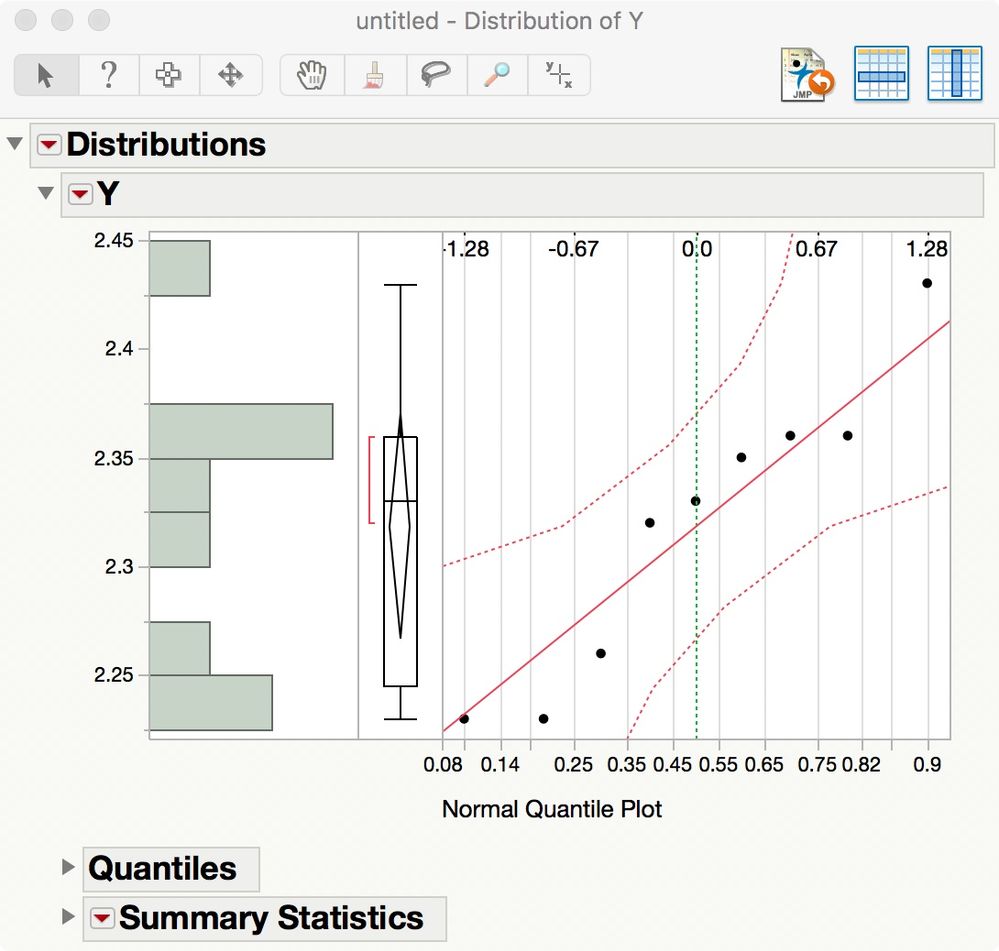
The normal quantile plot does not indicate two populations. That is, a model based on a single normal distribution appears adequate:

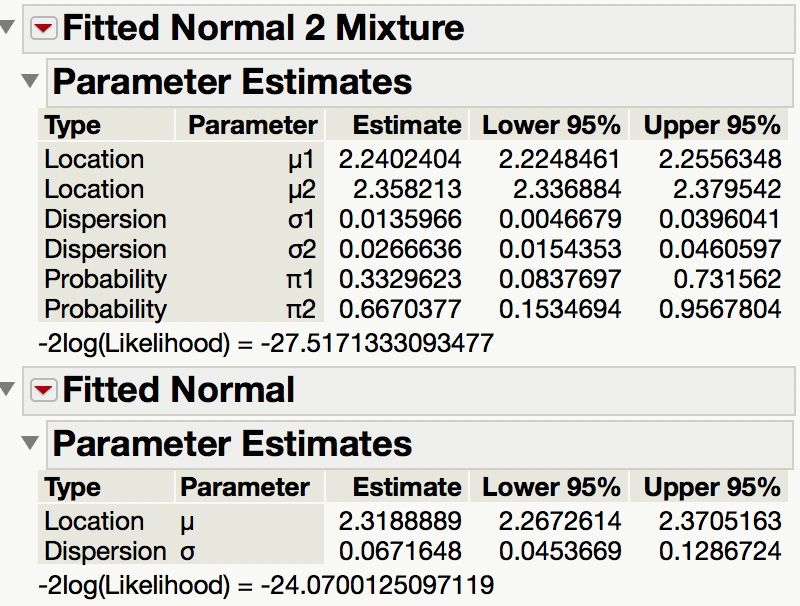
You could fit a mixture model based on two normal distributions:

The better model is the one with the smallest -2L. AICc is a better criterion because it includes a penalty for over-fitting. AICc is computed as -2L + 2k +2k(k+1)/(n-k-1) where k is the number of parameters and n is the sample size. The AICc for the normal distribution model is -24.0700125097119 + 2(2) + 2(2)(2+1)/(9-2-1) = −18.0700125097. The AICc for the normal mixtures distribution model is -24.0700125097119 + 2(6) + 2(6)(2+1)/(9-6-1) = 5.9299874903.

So a naive comparison based on -2L would select the normal mixtures model, the penalized criterion easily selects the simpler normal distribution.

The normal quantile plot shows no indication of a statistical outlier. If you know the contamination process, then a selective outlier detection test may be applied. Otherwise, you would have to use a general outlier test. Such a test would not be significant in this case.

[#5]

Hi Mark,

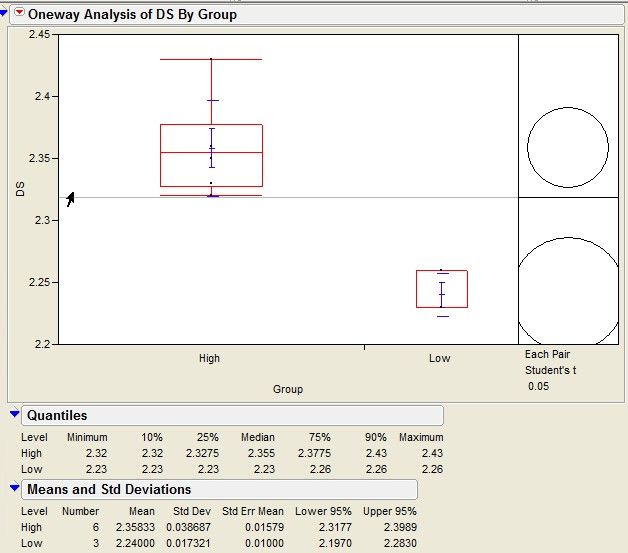
thanks again for the reply, here is how i compare the two group of DS, basically I have group the ~2.2 into one group while the one above ~2.3 in another group and perform the t-test to compare the mean. From the t-test is shows that the two are from two different population.  

 

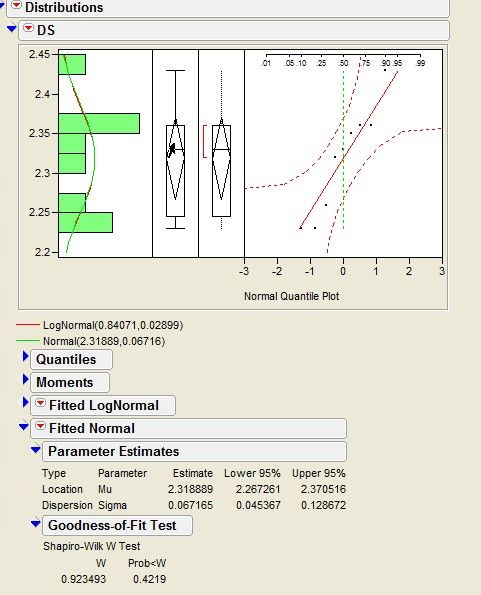
Here is my quantile plot, based on the shapiro wilk test can I say that the population of my sample is from a normal distribution.

Based on the normal quantile plot can I say that the 2.2 is coming from the same population as the rest?This is the question that I need to answer

THank you in advance for your explanation

[#6]

You can't have it both ways.

The analysis of the 9 observations with the normal quantile plot to determine if an extreme value is an outlier is invalid if you have already determined that there are two populations with respect to the mean parameter. You can't use a mixed sample this way for a valid conclusion. You must evaluate the potential outlier against only the observations in the sample from the same population (sample size is 3).

Funny that your goodness of fit test does not reject the single normal distribution model but your t-test did reject that the two groups have the same mean.

Anyway, you must not analyze the distribution of the 9 observations as a single population now that you established that there are two populations. You should separately examine the normal quantile plot for each population. You can use the Group column in the By analysis role in the Distribution launch dialog.

What is the basis for assignment of an observation to Group = Low or Group = High?

[#7]

Hi mark,
Thanks for the fast response, i guess my original question to the problem is whether the 2.2 value is coming from the same population as the 2.3, i actually segregrate the two groups based on my assumption that they belong to a different group. What is the correct way to approach this problem, can i say that they belong to the same normal distribution ?

[#8]

Are you asking if a single value (2.2) is coming from the same population? Then follow my last suggestion of using the normal quantile plot with the DS=Low observations.

Are you asking if the group of Group=Low observations come from the same population as the rest (Group=High)? Then use the t-test result.

[#9]

Yes, i would like to know what is the best statistical method to determine whether 2.2 is from the same population as the rest, a normal quantile plot should do?

[#10 · Accepted solution]

I suggest that you use an outlier test. Many tests have been developed for specific contamination processes. We know nothing about your contamination process so we can't use one of those tests. We must fall back to one of the less specific tests. You can find two of the most popular tests here in the File Exchange area of the JMP Community. I have included a link for both of them here:

• Dixon Q Test for Outliers
• Grubbs' Outlier Test

Be sure to carefully read the description before you use either one of them for an explanation and instructions.