Dixon Q Test for Outliers (Updated)

[#1]

(Please note that a problem was discovered with the original version of the script that was made available before 09Oct2014. The problem occurred when the sample size was greater than 30. has been corrected and the updated of the version replaced. The available tables of critical values only go to a sample size of 30, so the critical value for sample size 30 is used for all sample sizes greater than 30.)

(Please note that a another problem was discovered with the version of the script made available before 25Nov2017. The problem occurred by skipping the case for the computation of the Dixon q statistic for the single upper outlier by R10. Credit to user Julie Grender for identifying this problem and bringing it to our attention.)

(Please note that other problems were discovered with the version of the script made available before 19Sep2022. The problems occurred by miss-labeling the Dixon q statistic for the single upper outlier by R10  and by a missing decimal point in one of the critical quantile values. Credit to user Anne Siekhaus for identifying this problem and bringing it to our attention. The suggestion to identify the outlier was added as well. The data value and row number are now provided in the expanded report.)

This script implements the outlier tests by Dixon. The chosen test is appended to a Distribution platform. These tests are intended for small samples of data, where n is no more than 30. These tests are not intended to be used repeatedly or iteratively with the same data sample.

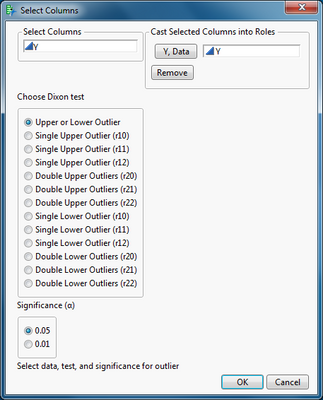
Simply open the data table with the data column suspected to include an outlier. (Note it is a good idea to examine the data with the Distribution platform before applying a test. The presence and nature of the suspected outlier will suggest an appropriate choice of the Dixon test.) Select the data column and click Y, Data. Select the appropriate test and the desired level of significance.

Click OK.

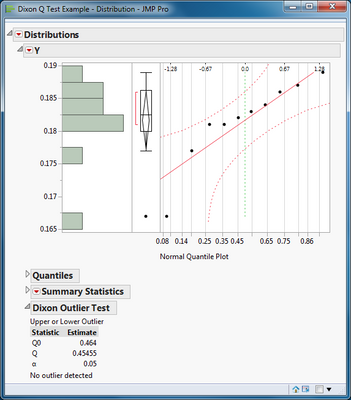
Q0 is the critical value of the statistic. A sample statistic Q that is greater than the critical value is significant. The test for an extreme outlier (low or high) was not significant at the 0.05 level.

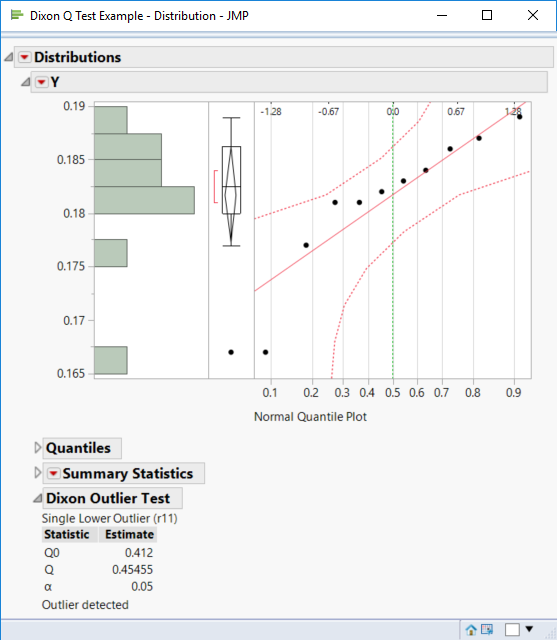
A different test (single low outlier) is significant in this case.

References

(1) R. B. Dean and W. J. Dixon (1951) Simplified Statistics for Small Numbers of Observations. **bleep**. Chem., 1951, 23 (4), 636–638.

(2) Barnett V. and T. Lewis (1994) Outliers in Statistical Data, 3rd Edition, New York: John Wiley & Sons.

[Jan]

Hi, thanks for the script.

It would be helpfull to also include in the output which value was actually considered an outlier
(or at least provide an indication whether it concerns the lowest or the highest value).

[DunnTiger764]

This is very poorly calibrated for n>30, since it uses critical values for n=30 for any larger n.  Critical values for n <= 30,000 were published a decade and a half ago.

http://satori.geociencias.unam.mx/index.php/rmcg/article/view/809 for n<=100
http://satori.geociencias.unam.mx/index.php/rmcg/article/view/673 for n<=1,000
http://satori.geociencias.unam.mx/index.php/rmcg/article/view/681 for n<=30,000

[DunnTiger764]

The last entry on line 220 is 341, but should be 0.341.

Dixon was optimistic on the accuracy of his interpolation, such that his published critical values can be wrong in the 2nd significant figure. Of the values use in this script, the worst is the n=9 alpha=0.01 critical value for r21, which should be 0.756 instead of 0.776, as shown by a massive simulation in http://satori.geociencias.unam.mx/index.php/rmcg/article/view/809 

[Anne_S]

Hi,

could you please check if there is an error in the script or if there is something I'm doing wrong:

When testing an n=5 sample, I can select "single upper outlier (r10)" and the result is correctly reported for this test. But when I select "single lower outlier (r10)", the result is reported for "single lower outlier (r11)" instead. Is this just a typo, or is the result actually reported for a different test than the one I selected?

Thanks & best regards

Anne

[Mark_Bailey]

@Jan, the outlier is identified in the Normal Quantile Plot. You can directly interact with the markers in the plot to identify the observation (row number by default) or select it.

The original row is lost in the computation after omitting excluded and missing observations, and sorting the remaining data. The identity of the outlier is tracked and reported now - thanks for the suggestion.

[yasmine_hajar]

Hello Mark,

Is there a plan to incorporate this script into JMP in an upcoming version?