- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Robust process setting with a categorical noise effect
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Robust process setting with a categorical noise effect
With profiler it is not possible to use a categorical noise effect? Is there another way to specify robust process settings?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Robust process setting with a categorical noise effect
Hi @frankderuyck,
From what I understand from your situation, there may be several options available :
- You can consider your categorical factor as a random effect (or noise), as you're interested on the variance caused by this factor, not by the change on the mean response.
- You can also use the Simulator, to add random noise to a categorical factor and assess how this may change the response distribution.
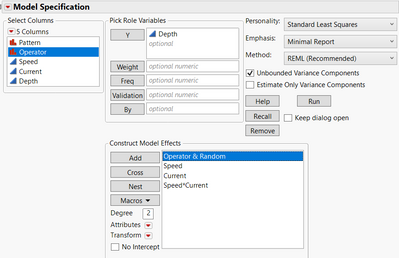
For the suggestion 1), I used the sample dataset "DOE Example 1" in the JMP sample index (in DoE). I changed the design role property of "Operator" to "Random Block", and run a model with the following effects :
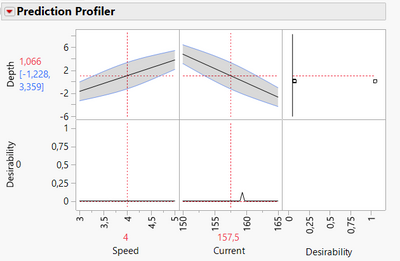
I end up with a Profiler that takes into account the variability introduced by the random effect "Operator" :
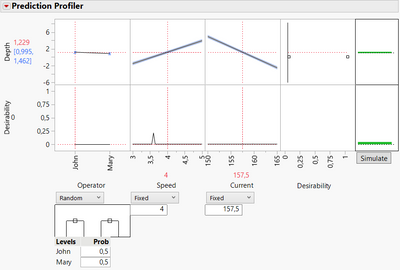
If using the profiler with Operator as a categorical fixed effect (or if set up as random effect, I can click on the red triangle next to the profiler, and make "Operator" factor appears by clicking on "Conditional Predictions"), I can use the Simulator, specify the type of noise (here I choose "Random" with a probability of 50% for each operator) and then click on Simulate :
The two approaches are conceptually different (a random effect suppose that these 2 operators are part of a bigger, unknown population which may also impact the variance of the results, whereas the Simulator uses only these 2 possible options to compute the results distribution) and lead to different results, so depending on your topic you may find one more relevant than the other.
I hope this will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Robust process setting with a categorical noise effect
Effects or Responses
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Robust process setting with a categorical noise effect
Find robust process settings for a categorical noise factor on a continuous response
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Robust process setting with a categorical noise effect
Hi @frankderuyck,
From what I understand from your situation, there may be several options available :
- You can consider your categorical factor as a random effect (or noise), as you're interested on the variance caused by this factor, not by the change on the mean response.
- You can also use the Simulator, to add random noise to a categorical factor and assess how this may change the response distribution.
For the suggestion 1), I used the sample dataset "DOE Example 1" in the JMP sample index (in DoE). I changed the design role property of "Operator" to "Random Block", and run a model with the following effects :
I end up with a Profiler that takes into account the variability introduced by the random effect "Operator" :
If using the profiler with Operator as a categorical fixed effect (or if set up as random effect, I can click on the red triangle next to the profiler, and make "Operator" factor appears by clicking on "Conditional Predictions"), I can use the Simulator, specify the type of noise (here I choose "Random" with a probability of 50% for each operator) and then click on Simulate :
The two approaches are conceptually different (a random effect suppose that these 2 operators are part of a bigger, unknown population which may also impact the variance of the results, whereas the Simulator uses only these 2 possible options to compute the results distribution) and lead to different results, so depending on your topic you may find one more relevant than the other.
I hope this will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Robust process setting with a categorical noise effect
Very useful Victor, thanks!
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us