- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Reporting W (or U values) for Wilcoxon mulit comparison
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Reporting W (or U values) for Wilcoxon mulit comparison
Is it possible to have JMP determine the W (or U) value? The out put for the Wilcoxon Method for multiple comparisons does not describe this which is disappointing.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Reporting W (or U values) for Wilcoxon mulit comparison
Like so much in statistics, there is seemingly a number of ways to get what you need. sebastianhoffmeister pretty much was on point with his response, and JMP indirectly reports the statistic that you need. As your question title implies, much like the Wilcoxon Rank Sums test itself, the U statistic is named depending on the source. After looking this up before answering your question I found that in the Wikipedia entry, which is for the Mann-Whitney U test, it is the U statistic. In a statistics textbook I have here in my cube (Ott and Longnecker, 5th ed.) it is referred to as the T statistic, but an example in the chapter on the Wilcoxon test has an example from Minitab where it is explicitly stated that the "test statistic W… is identical to the Wilcoxon T."
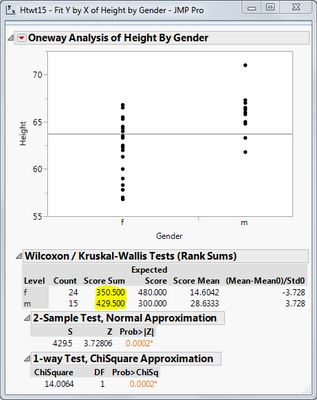
In JMP the Wilcoxon statistic is S that, according to JMP help, is the sum of rank scores. S is not U/W/T, but appears to be the greater of the score sums; note in sebastianhoffmeister's screenshot S = 429.5, the score sum of level m. the U statistics can be computed from the score sums, s1 and s2. If you refer to the Wiki entry, you will find that in sebastianhoffmeister's example, U1 = 50.5 and U2 = 309.5. According to the Wikipedia entry, U1 should be chosen, meaning the value of S would be 350.5, but JMP chooses the larger U statistic that also happens to be the larger score sum.
What I see in Ott and Longnecker does not indicate that either process is incorrect. The process for the Wilcoxon test according to that text is:
- List the data values for both samples from smallest to largest.
- Assign the numbers 1 to N to the data values with 1 to the smallest value and N to the largest value. These are the ranks of the observations.
- If there are ties—that is, duplicated values—in the combined data set, the ranks for the observations in a tie are taken to be the average of the ranks for those observations.
- Let T denote the sum of the ranks for the observations from Population 1.
The process does not set any requirement for which of the populations constitutes Population 1.
Another text that I have here (Milton and Arnold, 4th ed.), it states, "The test statistic… is the sum of the ranks associated with the observations that originally constituted the smaller sample." When I first learned about the Wilcoxon Rank Sums test grad school so that my research team could publish—getting called out for using a t-test on non-normal data sets during the peer review process for my very first submission was unpleasant to say the least—, I recall the texts that a stat professor loaned me on nonparametric statistics also mentioning that the score sums from the population with the smaller sample size should be used. This is what JMP also appears to be doing.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Reporting W (or U values) for Wilcoxon mulit comparison
As far as I know, there is no explicit way to do that in JMP. But of course JMP is reporting the score sums:
To get W you would just take the Minimum from those sums if I remember correctly.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Reporting W (or U values) for Wilcoxon mulit comparison
Thanks for the repsonse!
Gotcha, so I'd have to do them all pairwise instead of the multi-comparison method when dealing with large sets of Y responses.
Along those same lines and pardon my ignorance, but if I calculate a U value by hand 'U=((n1n2) + (n1(n1+1))/2)-R1' I do not get the same value as the score sum. I checked this value with a second software package and it was correct, just trying to not have to use multiple packages for the dozens of comparisons I'm trying to make. Thanks again
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Reporting W (or U values) for Wilcoxon mulit comparison
I started my other post before this response and it was late Friday afternoon
If you are trying to determine where differences exist when a footer has there or more levels, JMP can handle the pairwise testing for you with nonparametric statistical tests just as it does for an ANOVA. In the screenshot provided by sebastianhoffmeister, he provides a test on a factor with two levels. In that case running the Wilcoxon test (Nonparametric > Wilcoxon Test) provides two results: the normal approximation and the Chi-squared approximation. The previous is the result of the Wilcoxon Rank Sums test, whereas the latter is the result of the Kruskal-Wallis test. If you are fortunate enough to have JMP Pro, the results of the Exact test should also be shown. The Exact test should be used in place of the normal approximation when sample sizes are small (N ≤ 20).
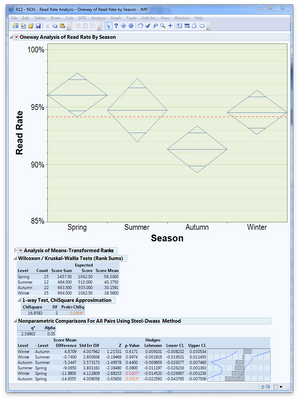
When your facts has only two levels, the result of the Wilcoxon Rank Sums test will let you know if there is a significant difference between the two levels. If you have more than two levels, the Kruskal-Wallis test will only inform you that at least one of your levels is significantly different. An example of nonparametric testing with more than two levels is shown below.
Note that there is no 2-sample test result (normal approximation). JMP does not display results for the Wilcoxon Rank Sums test in my example, as it is non-applicable. The result of the Krusal-Wallis test was that a season effect was detected (p = 0.0008), so I used the Steel-Dwass method for pairwise testing. The Steel-Dwass method is the nonparametric equivalent of the Turkey HSD (also known as the Turkey-Kramer method or Tukey's range test). In order to get the pairwise test results you go to Nonparametric > Nonparametric Multiple Comparisons where you will see a selection of nonparametric pairwise tests. For more information on these tests you can begin by referencing the JMP online help on nonparametric oneway analysis. The online help should have enough for you to get started in determining which pairwise test is applicable to your analysis.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Reporting W (or U values) for Wilcoxon mulit comparison
Like so much in statistics, there is seemingly a number of ways to get what you need. sebastianhoffmeister pretty much was on point with his response, and JMP indirectly reports the statistic that you need. As your question title implies, much like the Wilcoxon Rank Sums test itself, the U statistic is named depending on the source. After looking this up before answering your question I found that in the Wikipedia entry, which is for the Mann-Whitney U test, it is the U statistic. In a statistics textbook I have here in my cube (Ott and Longnecker, 5th ed.) it is referred to as the T statistic, but an example in the chapter on the Wilcoxon test has an example from Minitab where it is explicitly stated that the "test statistic W… is identical to the Wilcoxon T."
In JMP the Wilcoxon statistic is S that, according to JMP help, is the sum of rank scores. S is not U/W/T, but appears to be the greater of the score sums; note in sebastianhoffmeister's screenshot S = 429.5, the score sum of level m. the U statistics can be computed from the score sums, s1 and s2. If you refer to the Wiki entry, you will find that in sebastianhoffmeister's example, U1 = 50.5 and U2 = 309.5. According to the Wikipedia entry, U1 should be chosen, meaning the value of S would be 350.5, but JMP chooses the larger U statistic that also happens to be the larger score sum.
What I see in Ott and Longnecker does not indicate that either process is incorrect. The process for the Wilcoxon test according to that text is:
- List the data values for both samples from smallest to largest.
- Assign the numbers 1 to N to the data values with 1 to the smallest value and N to the largest value. These are the ranks of the observations.
- If there are ties—that is, duplicated values—in the combined data set, the ranks for the observations in a tie are taken to be the average of the ranks for those observations.
- Let T denote the sum of the ranks for the observations from Population 1.
The process does not set any requirement for which of the populations constitutes Population 1.
Another text that I have here (Milton and Arnold, 4th ed.), it states, "The test statistic… is the sum of the ranks associated with the observations that originally constituted the smaller sample." When I first learned about the Wilcoxon Rank Sums test grad school so that my research team could publish—getting called out for using a t-test on non-normal data sets during the peer review process for my very first submission was unpleasant to say the least—, I recall the texts that a stat professor loaned me on nonparametric statistics also mentioning that the score sums from the population with the smaller sample size should be used. This is what JMP also appears to be doing.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us