- Due to inclement weather, JMP support response times may be slower than usual during the week of January 26.
To submit a request for support, please send email to support@jmp.com.
We appreciate your patience at this time. - Register to see how to import and prepare Excel data on Jan. 30 from 2 to 3 p.m. ET.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Repeated randomized 4 by 4 latin square
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Repeated randomized 4 by 4 latin square
I have a field setup with 4 treatments in a latin sqaure setup repeated 5 times.
A B D C
C A B D
B D C A
D C A B
This field setup is enclosed.
The setup is repeated 5 times but randomized between each run.
9 animals are released into an enclosure and can freely choose from all of the treatments. The number of times an animal visit a treatment is recorded and summarized for a period of times (1 hour) for each repeated setup.
The same 9 animals are used between the 5 repeats.
My guess that the animal (ID) within each repeat sjould be random effect.
I want to know if there is significant differences in use of treatment. Maybe not between the animal nor between the repeated setups.
What is the correct methods to analyse this in JMP?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Repeated randomized 4 by 4 latin square
This is not a Latin Square design. You might have selected a Latin square for the layout of the grid but the design and associated analysis are for experiments that run one of the sixteen treatments at a time over changing levels of two blocking factors. (See the JMP table that I provided for a Latin Square experiment.) The design supports the linear model that decomposes the fixed effects of the three factors and accounts for the single source of random errors.
Instead, you are simultaneously presenting sixteen locations labelled A-D in a grid, recording the location of nine animals at regular intervals and accumulating the counts. I have seen neither such an experiment nor the model for the data analysis. If this approach is common in your field, then you might consult a reference or expert to discern the model. If you can tell us the data set layout and the model, then we can help you analyze it in JMP.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Repeated randomized 4 by 4 latin square
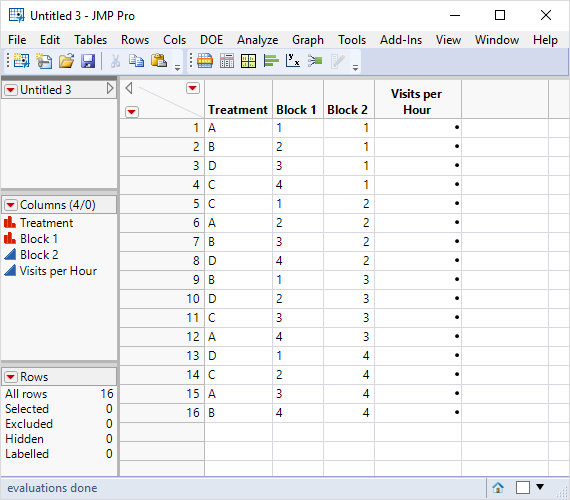
The response is the number of visits in a one hour run. You have one categorical factor with four levels (A, B, C, D). You have two blocking factors each with four runs. (You did not specify the nature of the two blocking factors.) There are a total of sixteen runs times five replicates. Here is the set up of your Latin Square design in JMP for the proper analysis:
That might not be what you intend to do ("freely choose from all of the treatments"). The design presents one treatment at a time. Is that clear?
You could enter the replicate values in the same row and then stack these response columns before analysis or you could add four replicates of these rows and enter the observations in one column as shown.
It is not clear about how the nine subjects are used in this experiment ("9 animals are released into an enclosure "). Are they tested individually (one at a time) or together (nine at the same time)? The answer will determine how the effect of the animals enters the model.
See Help > Books > Fitting Linear Models for more details.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Repeated randomized 4 by 4 latin square
Hi.
Thank you for your reply.
All animals are released at the same time in the 4x4 enclosures. And every 10 sec the position of the animals in a given RxC (e.g. A1) are recorded.
Nicolai
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Repeated randomized 4 by 4 latin square
This is not a Latin Square design. You might have selected a Latin square for the layout of the grid but the design and associated analysis are for experiments that run one of the sixteen treatments at a time over changing levels of two blocking factors. (See the JMP table that I provided for a Latin Square experiment.) The design supports the linear model that decomposes the fixed effects of the three factors and accounts for the single source of random errors.
Instead, you are simultaneously presenting sixteen locations labelled A-D in a grid, recording the location of nine animals at regular intervals and accumulating the counts. I have seen neither such an experiment nor the model for the data analysis. If this approach is common in your field, then you might consult a reference or expert to discern the model. If you can tell us the data set layout and the model, then we can help you analyze it in JMP.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us