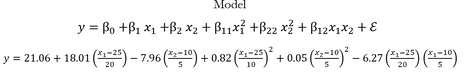- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Regarding the Prediction Expression
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Regarding the Prediction Expression
Hi members,
I am conducting an RSM design on jmp 16 and I want to extract the prediction expression for the model. This is the prediction expression I got.
The centre points for x1 and x2 are 25 and 10 respectively.
- I am trying to wonder why the variables are centred using the centre points for this type of model. (I thought it only applies to first-order models to account for curvature)
- When reporting this model in writing, should I leave the equation as it is?
Any help will be greatly appreciated. Thank you in advance.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Regarding the Prediction Expression
Hi,
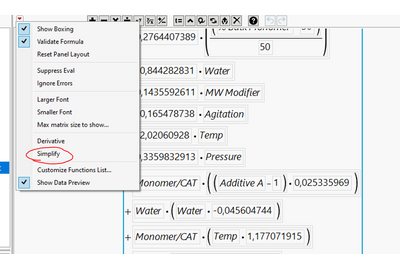
It may be helpful to know that you can covert the second expression to the first by saving the prediction formula to the table, opening it using the Formula editor and selecting "Simplify" from the red-triangle menu:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Regarding the Prediction Expression
There are many ways and reasons to transform variables. The transformation that you encountered is called 'coding.' It is considered a best practice when analyzing data from a designed experiment for several reasons. The JMP design platforms (e.g., Custom Design) add the Coding column property to the continuous factor data columns when you click Make Table. The Fit Least Squares platform recognizes this column property and internally applies the transformation.
Interpretation:
Without coding, the parameter estimates depend on the scale (i.e., measurement units). It is difficult to answer questions such as, "Which factor is the most important?" just by examining the estimates. On the other hand, coded factor levels lead to scale-invariant estimates. They still represent the change in the response for a one unit change in the factor, but now that is half the factor range for all factors. (For this reason, the estimate using coded factor levels are sometimes referred to as 'half effects.') Also, the intercept is usually necessary for modeling but meaningless. With coding, the intercept is always now the mean response at the origin of your design space.
Power:
We always want estimates with the smallest standard error, regardless of the purpose of the experiment (e.g., screening versus optimization). The design determines the correlation among the estimates. Uncorrelated estimates will have the smallest standard error. Correlation will inflate the variation of the estimates and, therefore, their standard errors. Perfectly correlated errors have infinite variance and are therefore inseparable. The effects represented by these parameters are confounded. Coding the factor levels minimizes the correlation among the estimates.
Stability:
Model hierarchy is related to coding. We strongly recommend that you maintain model hierarchy when you add or remove terms from the model. One reason is that the model will be unstable if you later change (transform) variables, such as reversing the coding transformation. Using the Simplify function in the formula editor as suggested by @HadleyMyers produces a different model (some terms vanish, new terms appear) if you do not maintain the hierarchy when selecting your model.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Regarding the Prediction Expression
Hi,
It may be helpful to know that you can covert the second expression to the first by saving the prediction formula to the table, opening it using the Formula editor and selecting "Simplify" from the red-triangle menu:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Regarding the Prediction Expression
Thank you for showing me the means to a simplified version of the regression equation. I am still new to regression modelling. I also wanted to know why we do not use the parameter estimates as they are. What is usually the reason behind centering the predictor variables using the centre points in the prediction expression?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Regarding the Prediction Expression
Hi @Kimani ,
When JMP performs the fitting, it will center the X factors by default (I think), unless you specify it not to. The reason is that the algorithm can determine a better estimate of the betas, the coefficients. Doing it this way helps to push a lot of the unknown error of the fit to the constant, epsilon, thereby reducing the errors of the fit estimates, the betas.
Hope this makes sense and helps,
DS
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Regarding the Prediction Expression
There are many ways and reasons to transform variables. The transformation that you encountered is called 'coding.' It is considered a best practice when analyzing data from a designed experiment for several reasons. The JMP design platforms (e.g., Custom Design) add the Coding column property to the continuous factor data columns when you click Make Table. The Fit Least Squares platform recognizes this column property and internally applies the transformation.
Interpretation:
Without coding, the parameter estimates depend on the scale (i.e., measurement units). It is difficult to answer questions such as, "Which factor is the most important?" just by examining the estimates. On the other hand, coded factor levels lead to scale-invariant estimates. They still represent the change in the response for a one unit change in the factor, but now that is half the factor range for all factors. (For this reason, the estimate using coded factor levels are sometimes referred to as 'half effects.') Also, the intercept is usually necessary for modeling but meaningless. With coding, the intercept is always now the mean response at the origin of your design space.
Power:
We always want estimates with the smallest standard error, regardless of the purpose of the experiment (e.g., screening versus optimization). The design determines the correlation among the estimates. Uncorrelated estimates will have the smallest standard error. Correlation will inflate the variation of the estimates and, therefore, their standard errors. Perfectly correlated errors have infinite variance and are therefore inseparable. The effects represented by these parameters are confounded. Coding the factor levels minimizes the correlation among the estimates.
Stability:
Model hierarchy is related to coding. We strongly recommend that you maintain model hierarchy when you add or remove terms from the model. One reason is that the model will be unstable if you later change (transform) variables, such as reversing the coding transformation. Using the Simplify function in the formula editor as suggested by @HadleyMyers produces a different model (some terms vanish, new terms appear) if you do not maintain the hierarchy when selecting your model.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Regarding the Prediction Expression
Thank you very much for the elaborative explanation @Mark_Bailey. The explanation will go a long way in helping me understand the regression model.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us