- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Life distribution - reliability projection
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Life distribution - reliability projection
Hello,
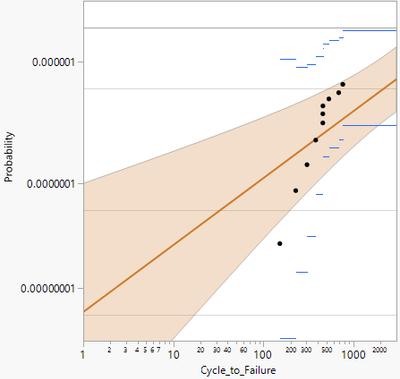
I have a set of time to even data and when I fit the life distribution, JMP provides the best distribution as Frechet with the following plot. The points seem to trend up and not nicely scattered around the line. How do I interpret this? This is supposed to be the best fit per JMP's choice.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Life distribution - reliability projection
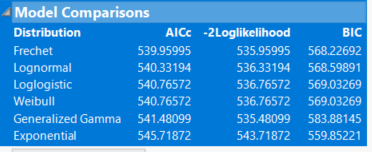
The best fit is not necessarily a good fit. The other fits are worse. There is a table of all the fits for comparison using criteria such as AICc. JMP presents the fits in ascending order of AICc (smaller is better).
Can you show this table for comparison? Can you show plots for the other fits that you entertained?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Life distribution - reliability projection
The best fit is not necessarily a good fit. The other fits are worse. There is a table of all the fits for comparison using criteria such as AICc. JMP presents the fits in ascending order of AICc (smaller is better).
Can you show this table for comparison? Can you show plots for the other fits that you entertained?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Life distribution - reliability projection
Hi Mark,
Thank you and here is the table you asked for:
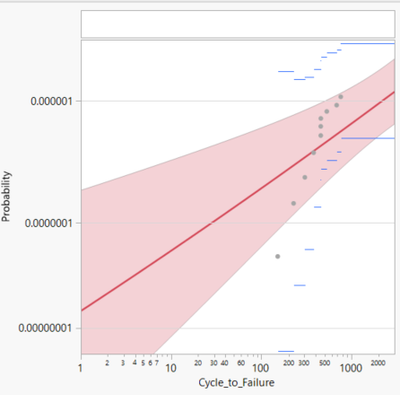
lognormal plot:
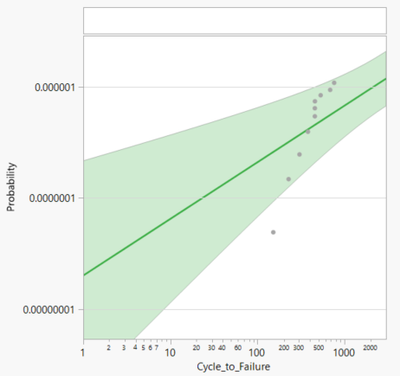
Weibull plot:
Cheers,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Life distribution - reliability projection
I noticed that the data plotted is not part of the current row selection in the data table. Is it possible that you have excluded rows that are plotted here? That row state would affect the fit a lot.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Life distribution - reliability projection
I noticed the probability values are extremely small. I also notice, there is a long horizontal segment at the end of the nonparametric estimate. I also have a feeling that it is probable that there is unlikely to have failures between 0 and 100.
Based on those observations, I suggest looking into two special types of distributions: Threshold distributions and Defective Subpopulation distributions. They are labelled as TH distributions, e.g. TH Lognormal, TH Weibull, etc. And DS distributions.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us