Least squares regression for nonlinear system of equations

[#1]

Hello - I have a moderately complex model for a physical process (ion adsorption for anyone who knows what that means). I have two starting variables, x1 and x2, and two measured outcomes, y1 and y2 that change with x1 and x2, and unmeasurable, or hard to measure, variables, g1,...,gn that don't change. One or both of x1 and x2 can also change for each row in a series. I have a set of nonlinear equations, s = f(x1, x2, y1,...,y2, g1,...,gn), as well as some other functions of different variables in f, depending on how complex I want the model to be. See the attachment for example equations.

The typical way we do this is in Matlab with lsqnonlin. Works well, but it's a bear to get running. I'd much rather have a (not-so-simple) column formula. However, I'm not entirely sure how to code it. The nonlinear regression thing is built for single equations, and with the three equations that all describe the same s, it seems like recursion would abound. I'm also not sure what the loss function would be. In matlab, we input guess values, calculate the least squares between the guess and the calculated value, update it if the sum of squared differences of all the guesses and equations falls outside some tolerance, and then loop. I'm assuming this is done internally by the nonlinear platform, but then is my target zero since I want the sum of squared differences to be zero? Or if not, how do I do multiple equations?

Apologizes if this is way simpler than I'm thinking.

[#2]

The limit is not in terms of number of parameters. But the number of parameters is a factor in your case. So, you have to try and see.

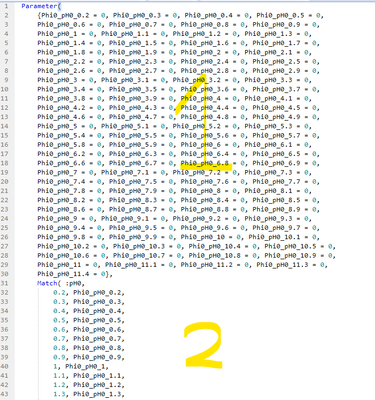
I see your system has three distinct types of parameters: Phi, sigma, pHf. They are all conditioned on value of pH0. Therefore, the parameters are independent by different pH0. So, you are right, do a "By" fit can reduce the complexity.

P.S. "By" is not working as I wished. All rows see all parameters in the column. I don't see it is possible to let individual rows in By to see just a subset of parameters.

I see the number of parameters after launching the Nonlinear. There is a able of parameters. I right click and create a table out of it, count rows. For the last two rows, I would suggest just edit the JSL formula. Open up the formula editor of the column. Copy it, and paste into a JSL editor. After editing, copy and paste back. By such, you can edit the list of parameters:

The "1" section is your list of parameters. The "2" is the actual formula.

[#3]

Follow up on how to use "By".

Seems there is a way to use By and reduce the number of parameters to take advantage of independence among rows.

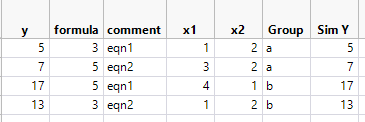
I attach v2 of the "nonsense system". First explain what I set up.

I set up two systems of linear equations. Row 1 and 2 are system "a", the Group column. And row 3 and 4 are system "b".

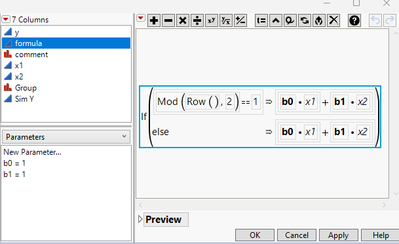
Each linear system has two parameters "b0" and "b1", but they are different between systems. And I use the parameters, x1, and x2 to produce "SimY". I copy SimY to Y for my analysis.

Now look at the "formula" column, I do not differentiate "b0" ad "b1" by Group.

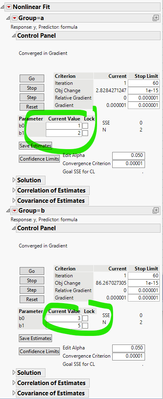
Now run Nonlinear with By = Group. And here is the report:

It finds separate, correct, solutions for respective systems.

[#4]

@peng_liu Yea I had run into the by issue as well. You're solution looks good! However, when I try to apply it to my table, it errors out. Do you see a glaring issue in the attached table? the Phi0, sigma0, and pHf are all the same as before. However, I made a "cyclic categorization" column for the "by" method you mentioned, but then have a "parameter by column". I use the levels of this column to expand parameters by categories. Since :Cyclic Categorization and :Parameter by column are orthogonal (or whatever the correct word is), this should allow the parameters to iterate over the whole curve at slight offsets (pH0 is the x axis), and then I can just put them together again at the end. However, like I said, its failing and only updating one of the levels of the parameters, and not sure why. 

Could this be an issue with how the by interacts with parameters expanded by categories? 

[#5]

You have missing values in Column3, which explains why only one group has result. But the "formula" is not set up as I recommended. I attach test.v2 to illustrate. With this approach, you no longer needs the Phi0, sigma0, and pHf in the middle.

[#6]

@peng_liu Oh duh. Not sure how I missed that many missing rows. Thanks for noticing that.

So maybe I'm misunderstanding, but since pH0 is my x axis, does your solution just mean the by column is the x column? like if you have 100 x values, you have 100 "groups" so to speak? 

If so, wouldn't the expanding by columns version be better since you are minimizing the error across multiple points rather than just a self contained minimization for each one? Or is point by point a better way to deal with loss functions? I'm kinda just fitting the matlab code I had to JMP, but don't really have expertise in minimization algorithms, so whatever the best technique is, I'm down for. 

P.S. And maybe I didn't make it clear, but there should be a unique set of values of each of the parameters for each pH0 value (which is the dependent variable). Which is why I thought I needed to expand by categories.

Thanks!

[#7]

I see your "formula" column in the original table depends on pH0. But the "formula" column in your test.jmp does not depend on pH0. I guess that is a misunderstand between us. Let me still use your original data, so Phi0, sigma0, pHf depend on pH0, not "Parameter by column".

Let's look at the first three rows:

Their pH0 = 0.2. Because of that, the formula of the first row can be denoted by:

f1(Phi0_pH0_0.2, sigma0_pH0_0.2, pHf0_pH0_0.2).

The 2nd and 3rd row formulas are:

f2(Phi0_pH0_0.2, sigma0_pH0_0.2, pHf0_pH0_0.2) and

f3(Phi0_pH0_0.2, sigma0_pH0_0.2, pHf0_pH0_0.2). The three rows form Group 1.

Now look at row 4, 5, 6. Their pH0 = 0.3. So the three formulas are:

f1(Phi0_pH0_0.3, sigma0_pH0_0.3, pHf0_pH0_0.3),

f2(Phi0_pH0_0.3, sigma0_pH0_0.3, pHf0_pH0_0.3), and

f3(Phi0_pH0_0.3, sigma0_pH0_0.3, pHf0_pH0_0.3). The three rows form Group 2.

Group1 and Group2 do not share same set of parameters. They are independent. Minimizing errors for Group1 has nothing to do with minimizing errors for Group2. So, we can optimize group by group.

If you keep parameter set in the three intermediate columns as Phi0_pH0_0.2, Phi0_pH0_0.3, Phi0_pH0_0.4, etc. each row sees all of them. You can see that if you run Nonlinear by pH0, and every group will have hundreds parameters listed. But among them, only three are relevant for each row, and every three rows.

What I did is creating three parameters only, inside of the column "formula". I named them paramPhi0, paramSigma0, parampHf. Even there are just three, when we run Nonlinear by "pH0", the platform will create different sets of the three parameters by "pH0". It literally creates those hundreds of parameters for you by "pH0". And each little Nonlinear by pH0 just need to worry about three parameters.

[#8]

I have some code that I use to model a moisture adsorption process - it seeks equilibrium conditions as described by multiple physical models - I'll see if I can make a generic version of the code that I can share on here.

[#9]

Hi @David_Burnham - yea if you had a generic version of that, that would be extremely helpful.