Intraclass Correlation

[#1]

Hi

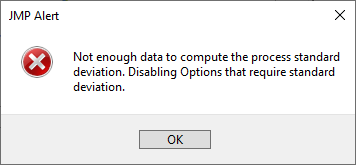
I need to compute the intraclass correlation for 2 readers who measured the same subject once each. I have rows of subjects with a column for each reader. It does not seem possible to do this with the MSA tool, which gives me an error when I try to use it (not enough information to compute standard deviation). SPSS does this with essentially one click (Reliability tool). Am I missing something?

thanks

Mark

[#2]

Is it possible to show us your data, or a mock up of your data? I am having trouble imagining your data. It would  help me answer your question. Thanks!

[#3]

So it's like

Case	Reader 1 Measurement	Reader 2 Measurement
1	0.556	0.578
2	0.213	0.256
...	...	...

[#4]

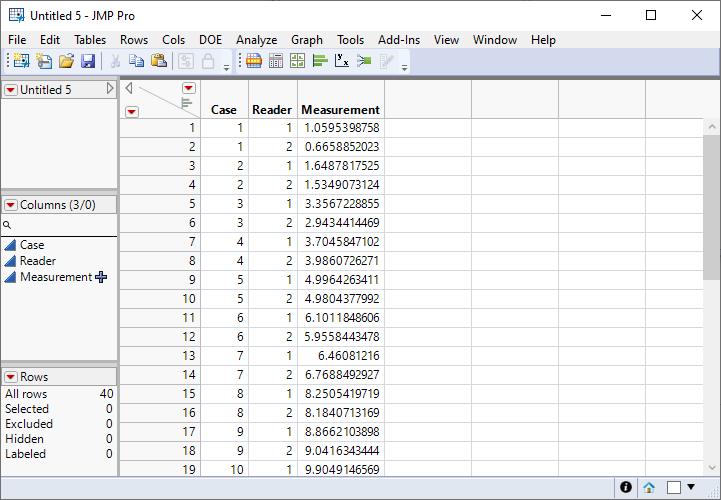
So it's set up in JMP like:

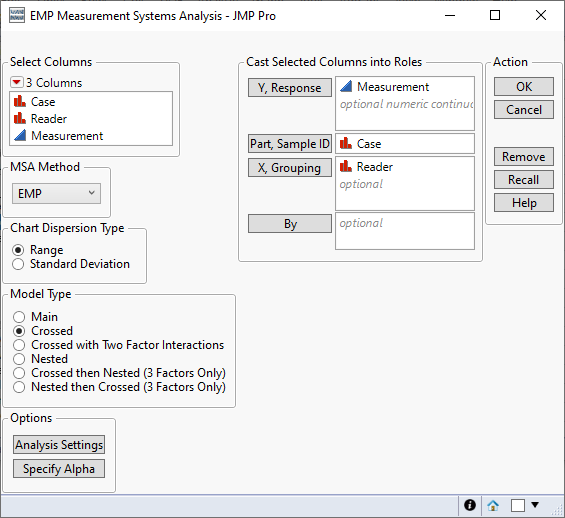
The table leads to the launch dialog:

I think that this alert is the one that you get:

The platform will launch and provide information, but it is limited by the lack of replicates that usually form the basis for estimating the repeatability or test-retest variation.

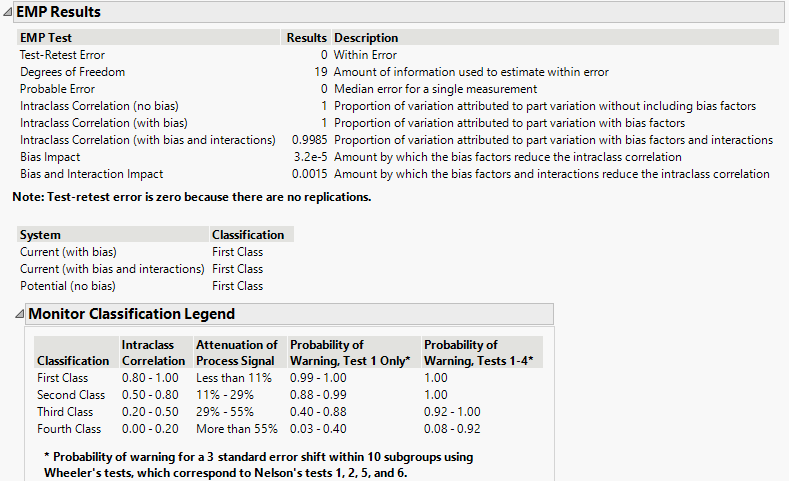
However, the ICC is still presented.

[#5]

So, first of all, it requires a re-formatting of the data into multiple rows per case instead of a single row, but that is manageable. However, the ICC reported as 1 is obviously incorrect. 

As I said, SPSS does the correct calculation, with essentially 1 click.

[#6 · Accepted solution]

I made a mistake. I should not include Reader as an analysis variable. Leaving Reader out, I get the following with my mock up of such data.

(In all honesty, I threw out the previous example and had to re-create it, so the simulation is not the same.) The MSA agrees with the ANOVA as suggested by @statman :

[#7]

My comments may not be useful, but here goes...you only have 2 readers, why not just do correlation using Pearson or Spearman (for non-parametric).  Multivariate Methods>multivariate.  You do not have any estimate of precision repeatability.  The same reader did not read the same case twice, so there is no estimate of this component.  Another way to say it is you have confounded precision repeatability with reproducibility.