- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Interval, different in JMP, LOGICALLY SHOULD BE SAME.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Interval, different in JMP, LOGICALLY SHOULD BE SAME.
Hi.
I faced a problem and appologize in advance that it might be a foolish question.
make simple, the situation is,
Data is
t={0,3,6,9,12}
y1={y11,y12,y13,y14,y15}
y2={y21,y22,y23,y24,y25}
y3={y31,....}
where y1,y2,y3 are the Batch number (Lot number)
So, there should be 3 respective regression line.
I tested the line comparability and the conclusion was "Different Slope and Different Intercept"
Thus, I put the Variables into the Model Fit platform as,
where G'=y and month=t.
The results were reasonable until the Confidence Interval is saved in Columns.
So far above method is method A.
However, by different way, method B,
Inputs are as follows,
The overall results seems SAME but,
Confidence Interval is DIFFERENTLY calculated from method A.
(you can focus only to the last row, comparing the values to the previous data figure... there is huge gap. 204 <> 247)
so, my question is,
where the reason lies for this difference?
To be honest, as I let JMP deals the DATA as "Different Slope and Different Intercept" (of course in case of both method A and B),
The Confidence interval should be look like the results of the method B.
Method A's Confidence intervals are so much alike among the batch 1,2, and 3.
Please help me.
Sorry for long story and english.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Interval, different in JMP, LOGICALLY SHOULD BE SAME.
Hi @MikeKim : It looks confusing to me because you have month as "Y" in the first Fit Model platform, and you have G' as "Y" in your second Fit Model platform. But, I assume that is a typographical mistake and you have G' as "Y" in both.
The first will be tighter because there are more degrees of freedom for error; i.e., building a single model as in your first dialog (method A) results in tighter confidence intervals because the sample size is larger. If you compare the degrees of freedom for error between the two models, you will see that error df (method A) is much larger than the error df for each lot (method B). In fact, error df (Method A) = the sum (over all the the lots) of the error df in Method B. This has a direct impact on the width of the confidence interval (makes it tighter).
Additionally, method A uses the pooled MSE (sort of an average MSE from across the lots).
For Method B, each lot has it's own MSE, and this that can make each lot have a different width as well for method B, even if the sample size etc is the same for each lot. .
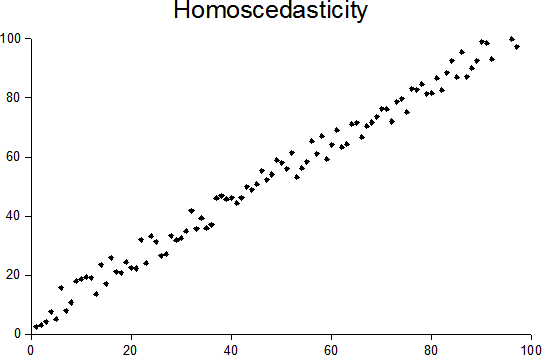
All said, Method A is the appropriate analysis (this assumes the MSE for each lot is approximately the same). If the MSE's are very different (you can get this from Method B) then Method B may be a better choice, unless you have JMP Pro and you can model heteroscedasticity (also known as heterogeneity of variance https://en.wikipedia.org/wiki/Homoscedasticity_and_heteroscedasticity). Graphically, you can assess this via looking at residual plots and/or regression lines to see of the spread around each lot is similar.
.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Interval, different in JMP, LOGICALLY SHOULD BE SAME.
Hi @MikeKim . Graph Builder is one of the more powerful platforms JMP has, and it is one of my favorites.
However, I can’t do it for you. And I don’t think it is possible to show you on this forum.
i can, however, tell you what additional columns etc you may need and point you to some resources.
1. In the Fit Model platform and the Fit Y by X platform, respectively as shown in figure 3, save prediction formula and confidence interval formulas. The confidence intervals for each batch from Fit Y by X will each use its own MSE. The confidence intervals for each batch from Fit Model will use the same Pooled MSE.
2. Add several rows to your data, but leave Y as missing. For these new rows, include batch and month. But, for each batch, the months should be months where you have no data. 1, 2, 4, 5, 7, 8, etc. This is so your final plots will look smoother.
3. Here is a resource for how to use Graph Builder. It may take some time and practice to get exactly what you want…but it will be time well spent.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Interval, different in JMP, LOGICALLY SHOULD BE SAME.
Hi @MikeKim : It looks confusing to me because you have month as "Y" in the first Fit Model platform, and you have G' as "Y" in your second Fit Model platform. But, I assume that is a typographical mistake and you have G' as "Y" in both.
The first will be tighter because there are more degrees of freedom for error; i.e., building a single model as in your first dialog (method A) results in tighter confidence intervals because the sample size is larger. If you compare the degrees of freedom for error between the two models, you will see that error df (method A) is much larger than the error df for each lot (method B). In fact, error df (Method A) = the sum (over all the the lots) of the error df in Method B. This has a direct impact on the width of the confidence interval (makes it tighter).
Additionally, method A uses the pooled MSE (sort of an average MSE from across the lots).
For Method B, each lot has it's own MSE, and this that can make each lot have a different width as well for method B, even if the sample size etc is the same for each lot. .
All said, Method A is the appropriate analysis (this assumes the MSE for each lot is approximately the same). If the MSE's are very different (you can get this from Method B) then Method B may be a better choice, unless you have JMP Pro and you can model heteroscedasticity (also known as heterogeneity of variance https://en.wikipedia.org/wiki/Homoscedasticity_and_heteroscedasticity). Graphically, you can assess this via looking at residual plots and/or regression lines to see of the spread around each lot is similar.
.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Interval, different in JMP, LOGICALLY SHOULD BE SAME.
Unfortunately, I cannot fully understand the solution.
Maybe since my explanation was not good enough
or my background is not enough to understand.
To be simple, my question was
method A and method B are both designated as "Different intercept, Common slope" (as it is the result of the 'degradation platform')
So, logically they should show the same result.
Obviously they don't and You are saying that there is An Other variable 'MSE' which impacts on the Width of CI?
and, seems like I cannot modify 'MSE' assumption while I using the JMP normal version?
My level of statistics is not graduated degree so, I really hope that I can understand following your further explanation.
Thank you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Interval, different in JMP, LOGICALLY SHOULD BE SAME.
Hi @MikeKim : I wasn't aware you were using the degradation platform. In the degradation (Stability Test) platform, choose the following option (Use Pooled MSE for Nonpoolable Model). This will do the right thing and result in tighter intervals. Does this make sense and is this what you are looking for?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Interval, different in JMP, LOGICALLY SHOULD BE SAME.
Hi, @MRB3855 :
Well, it is not sorry.
It is not natural to check 'Use pooled MSE' from the perspective of careful and naive analysis.
Basically, I want to base it on the results from the degradation platform.(Dif intercept, Com slope)
However, the CI curve in the degradation platform cannot exhibit the specific f(t) value except at the point where it meets the specification limit.
Therefore, the key point is to draw the same CI as the degradation platform through another platform.
The current problem is that neither method A nor method B that I introduced draws the same shape as the degradation platform.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Interval, different in JMP, LOGICALLY SHOULD BE SAME.
Hi @MikeKim : I tried some data of mine and the prediction intervals etc. were the same for both platforms. Can you provide pictures or data that show exactly what you are doing and what you comparing? The Model as you describe it is 'different intercept with common slope'. So, in the Fit Model platform you should have no interaction term; and in the Stability Platform you should always choose Use Pooled MSE for Nonpoolable Model as I described above (though this only makes a difference for the Different Intercept and Different Slope 'nonpoolable' model).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Interval, different in JMP, LOGICALLY SHOULD BE SAME.
hi, @MRB3855
Thank you for helping!
I tried to understand the entire content related to my issue and I failed.
Let me try to summurize and re-explain my question as following.
I am sorry I cannot attach real file.
fig 1
this is data
fig 2 degradation platform
left: Use Pooled MSE (Uncheck)
right: Use Pooled MSE (Check)
fig 3
left: fit y by x : alpha 0.1 CI is exactly same to the Pooled MSE(Uncheck)
right: fit model : Cannot draw CI figure
So, in summary, followings are my issues.
1. How do I consolidate the fig3 left into one graph containing 3 lines and respective CI??
2. How do I draw CI at the fig 3 right?
3. How do I apply the Pooled MSE to the fig 3 left and fig 3 right? (to the same figure as fig 2 right)
4. There is Save Column option (in red triangle) in fig 3 right (to see the CI value in table)
However, they always fixed to alpha=0.05, in this case I need alpha=0.1 since the original Degradation shows 0.1 CI.
So, how do I change alpha 0.05 to 0.1 in fig 3 right? (please check this at fig 4 below)
5. What is the practical explanation (practical meaning in laboratorial field) of Checking the Use Pooled MSE?
(The answer to the question from the colleague, "what is the using pooled mse?")
fig 4
Thank you so much!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Interval, different in JMP, LOGICALLY SHOULD BE SAME.
Hi @MikeKim : I will try to address these questons.
Fig 2: this is at it should be.
Fig 3: this is as it should be (the Fit Model platform does not show the confidence intervals)
1. How do I consolidate the fig3 left into one graph containing 3 lines and respective CI?? You will have save the predictions and intervals to your data table and use graph builder. That will be the same as Figure 2 left..
2. How do I draw CI at the fig 3 right? You will have save the predictions and intervals to your data table and use graph builder.
3. How do I apply the Pooled MSE to the fig 3 left and fig 3 right? (to the same figure as fig 2 right). Again, you will have save the predictions and intervals to your data table and use graph builder.
4. There is Save Column option (in red triangle) in fig 3 right (to see the CI value in table)
However, they always fixed to alpha=0.05, in this case I need alpha=0.1 since the original Degradation shows 0.1 CI.
So, how do I change alpha 0.05 to 0.1 in fig 3 right? (please check this at fig 4 below). In the Fit Model dialog, there is a red triangle next to Model Specification. If you click on that you can "set alpha level".
5. What is the practical explanation (practical meaning in laboratorial field) of Checking the Use Pooled MSE?
(The answer to the question from the colleague, "what is the using pooled mse?"). I explained MSE pooling in my initial response. The MSE is the Mean Squared Error. It is an estimate of the variance, and the variance is the
(Standard Deviation)^2. Each line has it's own MSE. The MSE for each line is the (Sum of Squared Errors)/(N-2). The Sum of Squared Errors (SSE) is the sum of squared differences between the line and the data. SSE is the sum of squared residuals. See plot below.
So, if the spread of data around the line is tight, then MSE will be very small (like the blue batch in fig 2). If the spread of data around the line is larger, then MSE will be larger (like the red batch in fig 2).
Pooling the MSE's can be thought of taking an average of the MSE's to attain a "pooled MSE" for the purpose of calculating confidence intervals etc. If you don't pool, each batch will use it's own MSE to calculate the confidence intervals via the equation below.
So, is it best to pool? Well, it depends. From a statistical perspective, if the MSE's are similar, then pool. If they are not similar, then you should try to understand why. Looking at your data, the blue batch seems much less variable (much lower MSE than the other batches) so pooling may not be appropriate. If you pool the MSE's, the width of the three intervals (around each batch) will be the same (each using the pooled, or "average", MSE), and will not reflect the fact that the blue batch is less variable. If you don't use pooled MSE, then the blue batch will have much tighter interval (as shown in figure 3 left) because it uses it's own MSE.
I hope I've understood your questions, I hope I've been helpful...and I hope there aren't too many typos!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Interval, different in JMP, LOGICALLY SHOULD BE SAME.
Hi, @MRB3855
I cannot find how I appreciate this help.
I found many knowledge and I am so happy.
However unfortunately, I have no experience with the Graph Builder.
So far I got to this point (from the Degradation platform with Use Pooled MSE checked), I know where the Graph Builder platform,
and having no idea how to draw the lines and CIs.
Would you mind to help me lastly?
Thank you so much!!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Interval, different in JMP, LOGICALLY SHOULD BE SAME.
Hi @MikeKim . Graph Builder is one of the more powerful platforms JMP has, and it is one of my favorites.
However, I can’t do it for you. And I don’t think it is possible to show you on this forum.
i can, however, tell you what additional columns etc you may need and point you to some resources.
1. In the Fit Model platform and the Fit Y by X platform, respectively as shown in figure 3, save prediction formula and confidence interval formulas. The confidence intervals for each batch from Fit Y by X will each use its own MSE. The confidence intervals for each batch from Fit Model will use the same Pooled MSE.
2. Add several rows to your data, but leave Y as missing. For these new rows, include batch and month. But, for each batch, the months should be months where you have no data. 1, 2, 4, 5, 7, 8, etc. This is so your final plots will look smoother.
3. Here is a resource for how to use Graph Builder. It may take some time and practice to get exactly what you want…but it will be time well spent.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us