Hi All,
Several questions regarding linear mixed models.
1) In the "Fit Mixed" personality is there a way to get the prediction expression (Y=Bx+Zu+E), I can get it from other model personalities but can't find it in the "Fit Mixed" personality
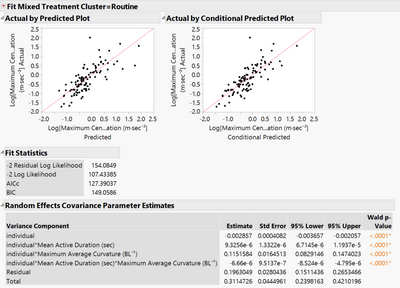
2) I am looking at swimming performance in fish, I have two continuous fixed effects and their interaction fit against a continuous response with individual and all its interactions selected as random effects (in total 3 fixed effects:2independent and 1 interaction and 4 random effects)
2a) when I am interpreting the random variance components is the residual in that table the variance left to be explained by the fixed effects?
2b) If I am getting significant random variance components and significant fixed effects are my fixed effects significant BECAUSE of the random covariance or INSPITE of the random covariance?
3) I am working with acceleration which appears to be non-linear and my model fits better when it is log transformed. Am I justified in transforming only acceleration and not my other continuous variables (which appear to be normal or nearly normal) or should I be transforming them all.
Here are a couple of screen grabs



Thanks in advance