- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Re:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How to calculate confidence intervals for multinomial proportions?
I have the following data:
20%
30%
40%
10%
Let's say for the type of a some product: a. b, c, d (respectively)
How to calculate confidence intervals for each proportion?
P.S. In this imitation example, we consider (for simplicity) that absolute numbers are also: 20, 30, 40 and 10 (total number: 100)
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to calculate confidence intervals for multinomial proportions?
Try running the distribution script in the attached version of your data. These instructions may also help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to calculate confidence intervals for multinomial proportions?
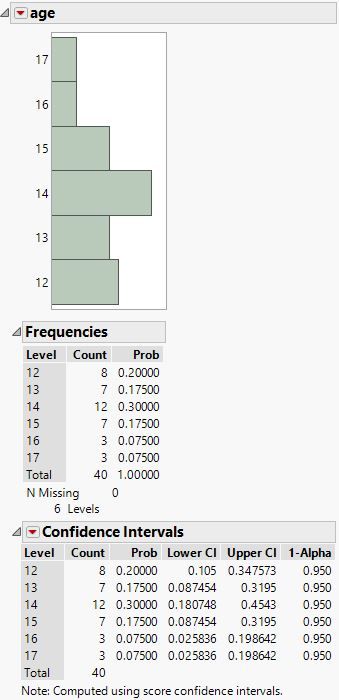
The Distribution platform will provide these intervals in a separate outline. Click the red triangle next to the name of the variable and select Confidence Intervals and the confidence level.
(Using the category age variable in Big Class for an example.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Re:
Click on the Green triangle next to the "Distribution of Group" entry in the Table Panel on the left side of the data table
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Re:
This short video will show how to run scripts from a data table: https://youtu.be/gz1AlTqQg7Q After watching that open the table I attached in my first reply and run the script saved to the table. If the report you get on running the script is the result you are after then open the link I gave in the first reply for instructions on creating the result you are after. This will guide you regarding the steps to take using the Distribution platform to recreate the results you are after.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to calculate confidence intervals for multinomial proportions?
I may be mistaken, but I don't believe most of the score procedures for confidence intervals referenced by the esteemed commentators are truly multinomial simultaneous confidence intervals.
If these are really multinomial proportions, I recommend reading the Sison and Glaz article from Journal of the American Statistical Association, Vol. 90, No. 429. (Mar., 1995), pp. 366-369..
Attached is a dataset of your example with some interval procedures compared in the article using formulae.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to calculate confidence intervals for multinomial proportions?
Attached, please find the Sison Glaz paper.
And, it might prove useful to have a quick explanation of the confidence intervals in the dataset...
QH = Quesenberrv-Hurst; G = Goodman; FS = Fitzpatrick-Scott
I have experience using the Goodman CIs for multinomials, and not so much with the others.
I'll include the reference for the Goodman intervals in another reply, since I cannot attach two files on one comment.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to calculate confidence intervals for multinomial proportions?
The Goodman reference, as promised.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to calculate confidence intervals for multinomial proportions?
Try running the distribution script in the attached version of your data. These instructions may also help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re:
Thank you, Malcolm! The instruction is important! Since I don’t practice scripts, say a few words, please, how to use your attached file.
Thank you, Mark, for pointing this!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Re:
Click on the Green triangle next to the "Distribution of Group" entry in the Table Panel on the left side of the data table
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Re:
This short video will show how to run scripts from a data table: https://youtu.be/gz1AlTqQg7Q After watching that open the table I attached in my first reply and run the script saved to the table. If the report you get on running the script is the result you are after then open the link I gave in the first reply for instructions on creating the result you are after. This will guide you regarding the steps to take using the Distribution platform to recreate the results you are after.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to calculate confidence intervals for multinomial proportions?
The Distribution platform will provide these intervals in a separate outline. Click the red triangle next to the name of the variable and select Confidence Intervals and the confidence level.
(Using the category age variable in Big Class for an example.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to calculate confidence intervals for multinomial proportions?
I may be mistaken, but I don't believe most of the score procedures for confidence intervals referenced by the esteemed commentators are truly multinomial simultaneous confidence intervals.
If these are really multinomial proportions, I recommend reading the Sison and Glaz article from Journal of the American Statistical Association, Vol. 90, No. 429. (Mar., 1995), pp. 366-369..
Attached is a dataset of your example with some interval procedures compared in the article using formulae.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to calculate confidence intervals for multinomial proportions?
Attached, please find the Sison Glaz paper.
And, it might prove useful to have a quick explanation of the confidence intervals in the dataset...
QH = Quesenberrv-Hurst; G = Goodman; FS = Fitzpatrick-Scott
I have experience using the Goodman CIs for multinomials, and not so much with the others.
I'll include the reference for the Goodman intervals in another reply, since I cannot attach two files on one comment.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to calculate confidence intervals for multinomial proportions?
The Goodman reference, as promised.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re:
Dear Kevin, I am overwhelmed with thanks... You have shown the complexity of this question. Thank you again...
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us