Full Factorial vs. Face Centered Response Surface Matrix

[#1]

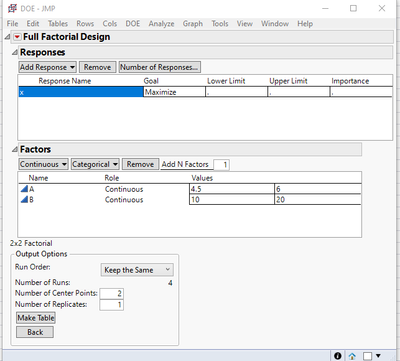
I have to factors and am trying to model a response. I only have 12 allowable runs and blocks are not an option here. I'm trying to figure which is the best approach here to optimize, assess curvature behavior and get the most out of the data. Here is my design:

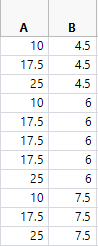
The resulting DoE (full factorial, 1 replicate, 3 center points) seems good but under Fit Model, it says I'm not to estimate quadratic terms. 

However, with a response surface matrix approach, I'm able to estimate quadratic terms, but with less replicates:

Also, this I-optimal design looks jsut like a 3x3 full factorial. I'm trying to understand the difference and which design would be the better approach. 

[#2]

Hi @sanch1,

Welcome in the Community

There are a lot of questions that can help you focus on the design choice that may be best suited for your needs. In your case, having 2 factors and a 12 runs experimental budget may be sufficient to get the most of your data. A few questions to get you started :

• Preliminary knowledge : Have you already some knowledge about your experimental space and factors influences, possible response surface topology ? Have you already done previous experiments ? Do you think the optimal configuration could be at the centre of your experimental space ?
• Response variability & noise : Do you suspect noise could be an issue ? Have you information about measurement precision, resolution and accuracy ? Will the experiments measured only by one operator/equipment or several ? 
• Objectives : What is your primary target ? Explore the experimental space, optimize, having a predictive model ? All ?
• Sequential/Fixed setting : Are you able to do sequential designs (to first assess possible interaction and curvature importance, and then optimize with perhaps a narrower factors ranges through a model-based or model-agnostic (Space-Filling) design) ? Or are you only able to do 1 design with 12 runs max ? 
• DoE & Modeling experience : What is your experience with DoE and modeling ? 

It's common good practice to test several designs, and compare the pros and cons of each through the Compare Designs Platform.

As for your question :

---

@sanch1 wrote:

The resulting DoE (full factorial, 1 replicate, 3 center points) seems good but under Fit Model, it says I'm not to estimate quadratic terms. 

---

Centre points are used to estimate curvature, assess response at the centre of the experimental space, and may provide lack-of-fit test. Since they are at the centre of the experimental space (hence the name), you can only fit one quadratic term with it/them (out of the two possibles in your study : X1X1 and X2X2).

Regarding your interest in replicates, it would be important for your design choice/decision to know if you suspect some important variability in your system. You may be able to use repetitions and replicates simultaneously :

• Repetitions is about making multiple response measurements on the same experimental run (same sample without any resetting between measurements). It doesn't add independent runs, you just measure the response several times, to reduce the variation from the measurement system (by using the average of the repeated measurements).
• Replication is about making multiple independent randomized experimental runs (multiple samples with resetting between each runs) for each treatment combination. It reduces the total experimental variation (process + measurements) in order to provide an estimate for pure error and reduce the prediction error (with more accurate parameters estimates).

Depending on where you think the highest variability may be and your experimental possibilities, you may choose one or both of these techniques.

I hope this first discussion starter may help you,

[#3]

Hi Victor,

Thank you for the response! I've provided some answers to your questions along with some further insight into what I'm trying to accomplish.

• Preliminary knowledge : Have you already some knowledge about your experimental space and factors influences, possible response surface topology ? 
  • These factors have been tested before, but in much lower part of the design space. This study aims to extrapolate from the previous work with values not yet tested. 
• Have you already done previous experiments ?
  • Yes, see above
• Do you think the optimal configuration could be at the centre of your experimental space ?
  • Good question. It's not yet clear what the "optimal" point is quite yet. 
• Response variability & noise :
• Do you suspect noise could be an issue ?
  • Yes. Previous data has shown this system behaves with a fair amount of noise in terms of response, 
• Have you information about measurement precision, resolution and accuracy ?
  • Somewhere in the range of ± 20% CV between repetitions has been observed
• Will the experiments measured only by one operator/equipment or several ? 
  • One operator, one piece of equipment.
• Objectives : What is your primary target ? Explore the experimental space, optimize, having a predictive model ? All ?
  • I'd say exploring the design space (i.e., finding any interactions between factors if they exist) and building a predictive model would be the primary goals. 
• Sequential/Fixed setting : Are you able to do sequential designs (to first assess possible interaction and curvature importance, and then optimize with perhaps a narrower factors ranges through a model-based or model-agnostic (Space-Filling) design) ? Or are you only able to do 1 design with 12 runs max ? 
  • Yes, sequential testing is an option here, albeit not ideal or cost effective. I was trying to get as much information as I can from one study given the constraints at hand.
• DoE & Modeling experience : What is your experience with DoE and modeling ? 
  • My experience has mostly centered around "first round" type of approaches: finding interactions, full factorial type of designs, design space exploration. However, I'm starting to get more into optimization and response surface modeling (in other words, what to do once you've identified significant factors)
• I have looked at the Compare designs platform with a few different designs I've come up with. Any help with what exactly to look for and how to interpret that report (power plot, prediction variance profile, fraction of design space).

Thank you for your help!

[#4]

Hi @sanch1,

Thanks for the responses.

Here are my thoughts :

• It may be interesting to include previous tests in the design, as it could help generalize the system behaviour in a large experimental window and may help provide more power for estimating main effects (as previous experiments across experimental space will be far). I would compare designs with and without these preliminary tests to assess the benefits of including them in the design generation. You can augment a design based on previous tests with the Augment Design Platform. and change factors range from your first runs if needed.
• Since you have some noise and the centre point may not be the optimal setting, it may be interesting to use replicates and repetitions to reduce experimental variance and allow a higher coefficients estimation precision. Setting the DoE ranges in a "bold" way can help : large factors ranges help in detecting main effects, as you can expect a higher difference in means between high and low levels despite the noise/variance, so statistical significance of these effects may be easier to detect.
• With only 2 factors in your DoE, you only have 6 effects to test for a quadratic model response surface : 1 intercept, 2 main effects, 1 interaction and 2 quadratic terms. Depending on if you expect all terms to be present or not, you have also the possibility to include some terms with Estimability set as "If Possible" instead of "Necessary" : Define Factor Constraints

Response surface models with quadratic and interaction terms are often sufficient to explain and optimize systems. In the case of complex systems or need for highly predictive models, the use of Space-Filling designs with Machine Learning algorithms can help to model irregularities or sudden changes/curvatures inside the experimental space.

For the Compare platform questions, you can see the rich documentation available here for explanation : Design Evaluation in the Compare Designs Platform

• Power Analysis  will help you compare the probability of detecting active effects if present, between several designs given the sample size, repartition of runs and assumed model. This is a good information for explanative model and/or model-based DoE focused on estimating coefficients precision (like D-Optimal designs) and help you assess and compare the chances of detecting specific effects across designs.
• Prediction Variance Profile will help you assess where your designs may have the larger prediction variance, so giving an intuition about the relative predictive abilities of the designs. Fraction of Design Space Plot also offers a concise comparative view on the predictive precision of your designs across the whole experimental space.
• I would also recommend looking at Design Diagnostics of your designs to better assess in which area(s) your designs are the most effective comparatively to each others : 
  • D-Efficiency refers to the ability to estimate precise coefficients for your model,
  • G-Efficiency refers to the ability of minimizing the maximum prediction variance (can be seen in the Prediction variance profile and Fraction Design Space plot)
  • A-Efficiency refers to the ability of minimizing the average variance of the estimates of the regression coefficients (can be seen in the Relative Estimation Efficiency panel)
  • I-Efficiency refers to the ability of minimizing the average prediction variance over the design space (can be seen in the Prediction variance profile and Fraction Design Space plot)

You can also create a large variety of designs possibilities (with various optimality criterion, number of runs, replicates, centre points, ...) through the Design Explorer platform and compare them quickly.

This is probably not a definitive answer to your questions and topic, but may hopefully help you imagine the design possibilities, compare them, and assess which one(s) are the most relevant for your use case.