- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Extend linear regression line in JMP version 13
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Extend linear regression line in JMP version 13
Hi,
I have a question regarding the Fit Line functionality in version 13.
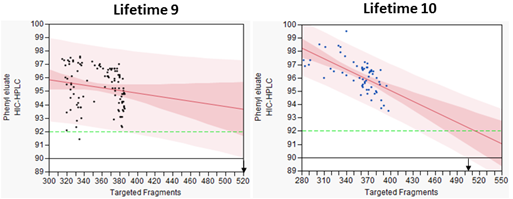
In version 10, I was able to make graphs with a linear regression line that extended beyond the data points (see figure). However in version 13 the linear regression line stops at the last data point. Is there a setting in version 13 to achieve the extension of the linear regression beyond the last data point?
Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Extend linear regression line in JMP version 13
Hi Julian,
The problem with your "trick" is this: Suppose I have a data table with three columns of data -- Age, Height, Weight. Sometimes I will plot Age vs Weight, sometimes I will plot Age vs Weight, sometimes I will plot Height vs Weight, and sometimes I will invert the X and Y values (Weight vs Age instead of Age vs Weight). Your trick works only if I have only a single X value for all plots. Correct? Or am I missing something? And, if I am correct, it becomes a real pain to manage as to which column (Age, Weight, Height) will be the X-value for the next plot that I will be making (or re-making via a script). Instead...JMP should -- at a minimum -- allow forced-fits (where I am prescribing the slope and intercept, for example) to extend to the limits of the X and Y plot window limits.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Extend linear regression line in JMP version 13
Hi @nocaltim,
I see just what you mean! There are a few ways to go about this. Using rows with value ranges staggered by column you can achieve the same result, regardless of what variable is the X or Y: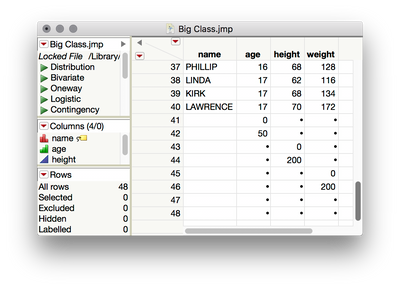
I hope this helps some!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Extend linear regression line in JMP version 13
This works acceptably on multiple data sets contained in the same column as split by a group column. this will work nicely although in JMP 14 I do look forward to seeing this operate by default.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Extend linear regression line in JMP version 13
I just need to say this, to get it out of my system. I understand there are exceptions to almost every rule, but:
1. Most physical phenomena are described by sums and/or products of differential equations. These differential equations are usually nonlinear in the parameters by nature. (This means something different than "curved"!!)
2. Since these sums and/or products of differential equations are very difficult to model, we tend to fit Taylor Series approximations to them, since they are much easier to specify and can often do an acceptable job of fitting the data. These approximations are necessarily fit only over the range of the existing data.
3. Making predictions by extrapolating these approximations outside the existing data is like playing Russian Roulette.
Please don't be too upset if JMP and the responsible denizens of this community don't want to help you load your gun!
You can do anything your heart desires, no matter how statistically ill-considered or exceptional, by writing a JSL script. Scripts can be easily deployed across an enterprise. You may wish to consider writing some JSL to implement your procedures.
Good luck!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Extend linear regression line in JMP version 13
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Extend linear regression line in JMP version 13
This has been one of my fustrations with the JMP program, as new rollouts have made the program less flexible and useable. If alternative work-arounds are being offered for functions that use to be available in past versions, then why was that functionality removed in the first place?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Extend linear regression line in JMP version 13
For large and complicated datasets the work-around is not feasible.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Extend linear regression line in JMP version 13
When first-generation food processors cut off fingers, responsible manufacturers added interlocks to the covers.
When Taylor Series approximations were improperly used to extrapolate beyond the range of the data, responsible manufacturers disabled that functionality.
I think Jim and Dan are right. Just say no to the workarounds. If you simply must extrapolate, fit a deterministic (usually nonlinear) model.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Extend linear regression line in JMP version 13
Regarding this issue of extending best-fit lines to the limits of the (say) X graph range limits, I would like suggest a scenario where it is very useful to have these best-fit lines extend beyond the data. In my work, EVERY SINGLE DAY I do an analysis where two variables should have perfect 1:1 correlation (slope of 1, intercept of zero). And this 1:1 correlation should extend across range that far exceeds my data limits. The actual X vs Y never a that true 1:1 correlation -- and that's very useful to know. But to help grasp this, I like to explicitly add the 1:1 line to the graph. And I want this 1:1 line to extend far beyond the data limits so that when I also do a best-fit on the actual data, even though the best-fit line is limited to the range of available data, I can use the 1:1 line as "tilted floor" of comparison. I fully understand why best-fit data shouldn't be extrapolated (too far) beyond the available data, but why can't I include an extended 1:1 line??? (Yes, I can add it as a graphical object, but that's just JMP *creating* work for me rather than JMP simlifying my work.) Comments?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Extend linear regression line in JMP version 13
While there are almost always exceptions to rules, I believe JMP has taken the most prudent road with the way they have implemented the platform.
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us