Deming analysis

[#1]

Hello,

I would like to compare two measurement methods using a deming regression.

This is a follow-up study, and in the first study my colleagues have used a deming regression in the "Analyze it" platform in Excel. But we don't have access to the software anymore, so instead I would like to conduct the analysis using JMP v. 16.  

As far as I understand, deming regression is not found in JMP?  

I have seen previous posts about using orthogonal fit if the variance ratio is 1. And I've also found an add-in from russ.wolfinger@sas.com.

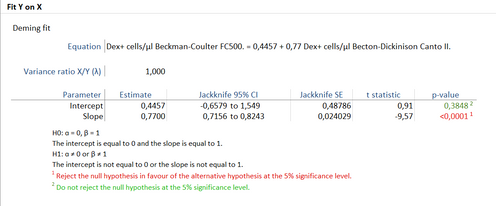
The Deming analysis output in "Analyze it" contains the slope, intercept, and CI and p-value for the slope and intercept. Moreover the CI values are Jackknife 95%.

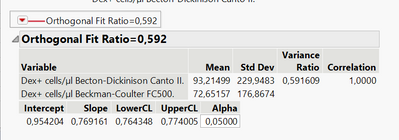
The output from Orthogonal fit in JMP only contains slope, intercept and confidence interval for the slope.

So, my question is how can I interpret the JMP output and determine if the two measurement methods are different without having the CI for the intercept and p-values for the slope and intercept. Do I need additional analyses, like Bland Altman in addition to the Orthogonal fit?

And are there better options in JMP for deming regression?

Thanks.

Br.

Dilek

[#2 · Accepted solution]

Yes, the orthogonal regression in the Bivariate platform is Deming regression. Alpha is set to 0.05 so the lower and upper limits are 95% confidence. The slope interval does not contain 1, so you decide that the two measurements are not equal.

Select Analyze > Specialized Modeling > Matched Pairs to see a Bland Altman analysis. That could answer the questions about the intercept not equal to zero, but you will find based on the result for the slope that it is not a constant bias, but a proportional bias.

You might also be interested in the MSA platform.

[#3]

Thank you - this is very helpful and answers my questions.