I generated independent probit regressions for multiple populations to a toxicant using a binomial general linear model with a probit link function and log(dose) as the X. Now I wish to convert my Y to probit units.
When I save formulae from the GLM output I get this formula for each population:
Normal Distribution(Intercept+Slope*Log(dose))
Given that a probit is the inverse of the cumulative distribution function I was thinking to make a new column with the formula:
(1) Normal Quantile(Normal Distribution(Intercept+Slope*Log(dose)))+5 *Note that the +5 is arbitrary
the output above seemed reasonable to me but I was confused to have both the normal quantile in addition to the normal dist in the equation and I would think that they would cancel each other and I decided to try the formula without the normal distribution as follows:
(2) Normal Quantile(Intercept+Slope*Log(dose)))+5
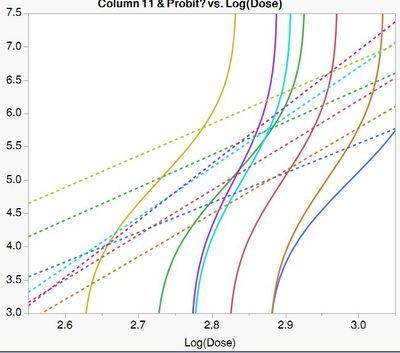
Once the "normal distirbution" is removed, as in (2), It dramatically influences the shape. Moreover, you can see the the 50% lethal dose (5 probits) changes depending on the equation, which is really important
Dashed lines are equation(1) and solid are equation (2) for each population.
Did I convert to probits correctly in equation 1? I have done a bit of research and have not seen mention of how to do this in JMP.
Thanks!
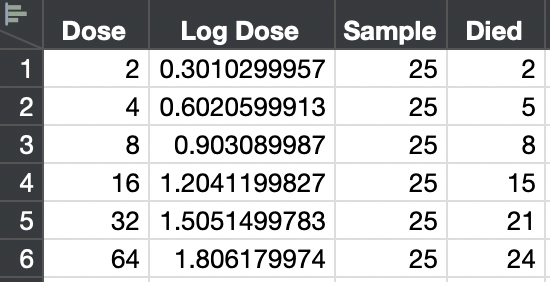
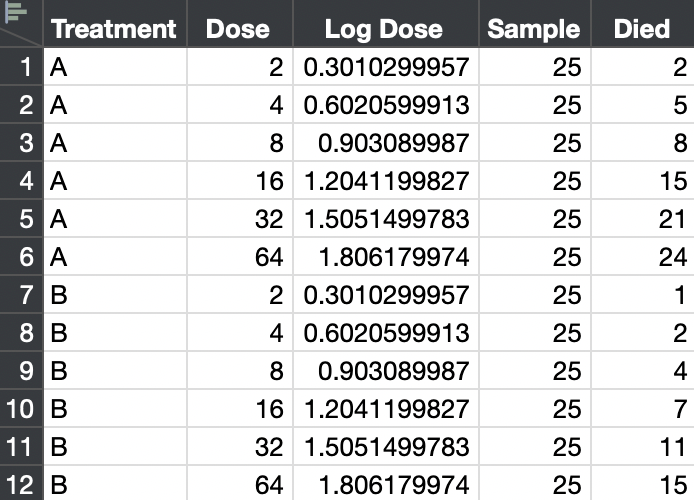
I honestly do not know what you mean by "probit units." Here is a mock up of a simple probit analysis. I created a test with increasing dose. There are 25 subjects for each dose. The number of deaths out of 25 is recorded.
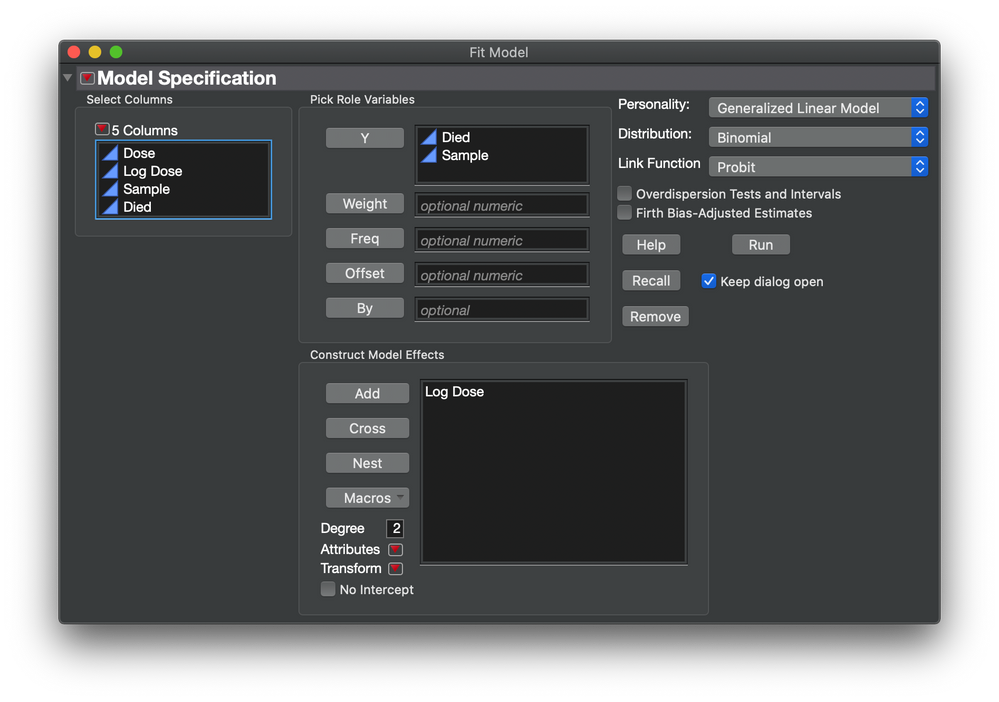
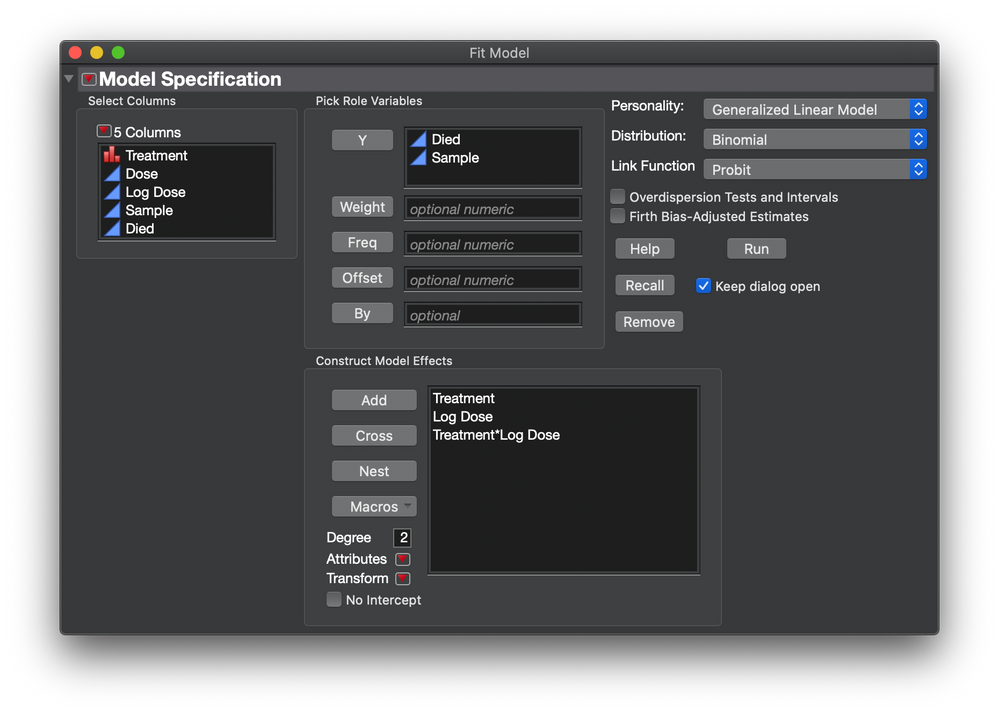
Next I started the probit analysis with this set up in the Fit Model launch dialog:
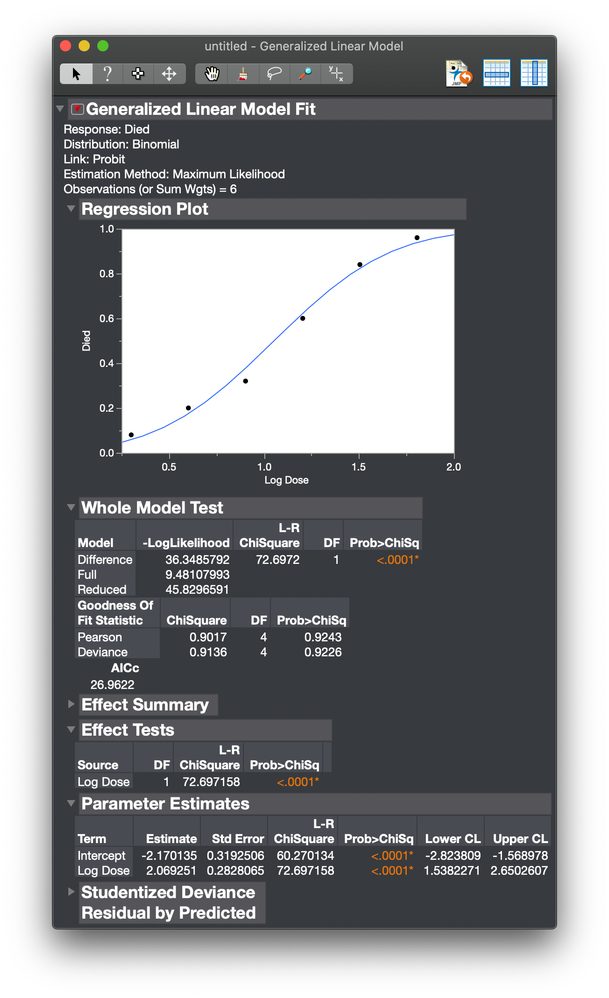
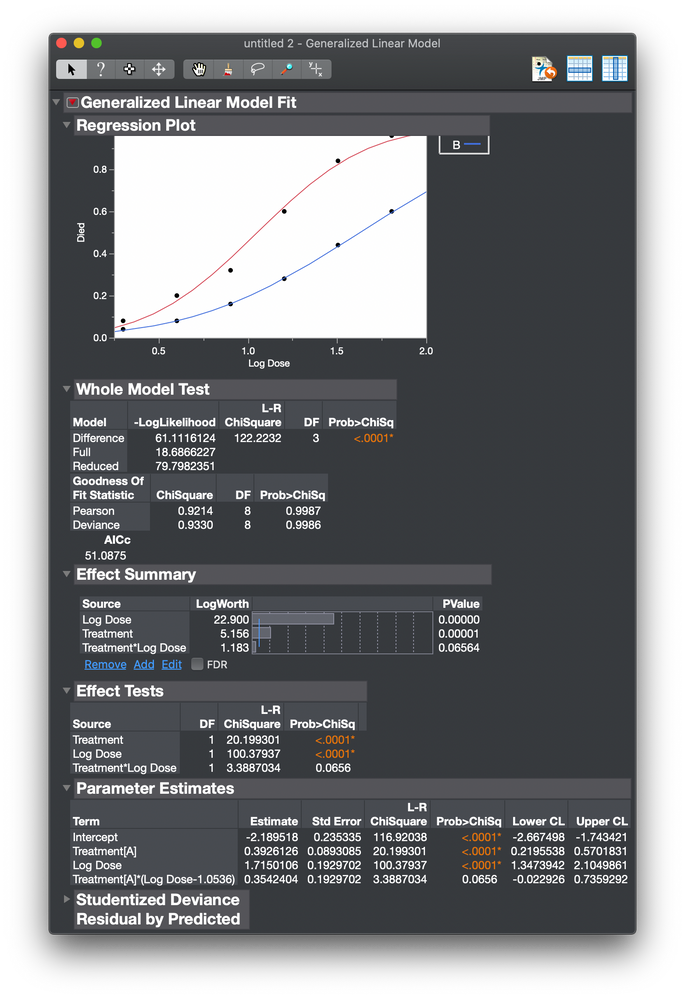
I then get this analysis.
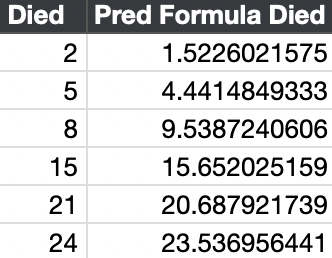
The plot shows the fitted probit curve as a function of Log Dose. The range of the probit function is 0 to 1. I saved the prediction formula to the data table.
The prediction formula is:
The predicted deaths is the sample times the probit or normal cumulative distribution function (CDF).
Is this quantity what you want? If not, please define "probit units" in terms of this example.
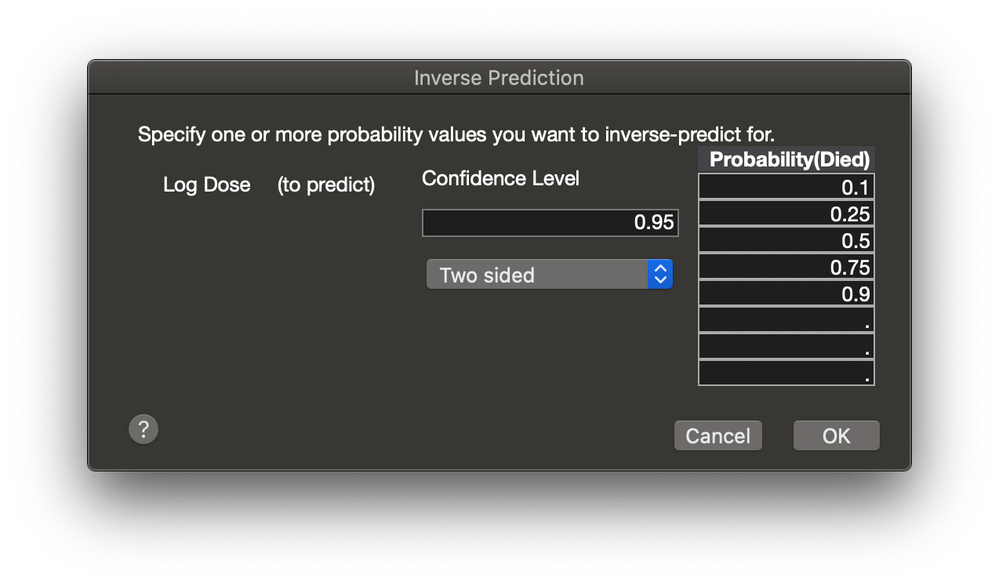
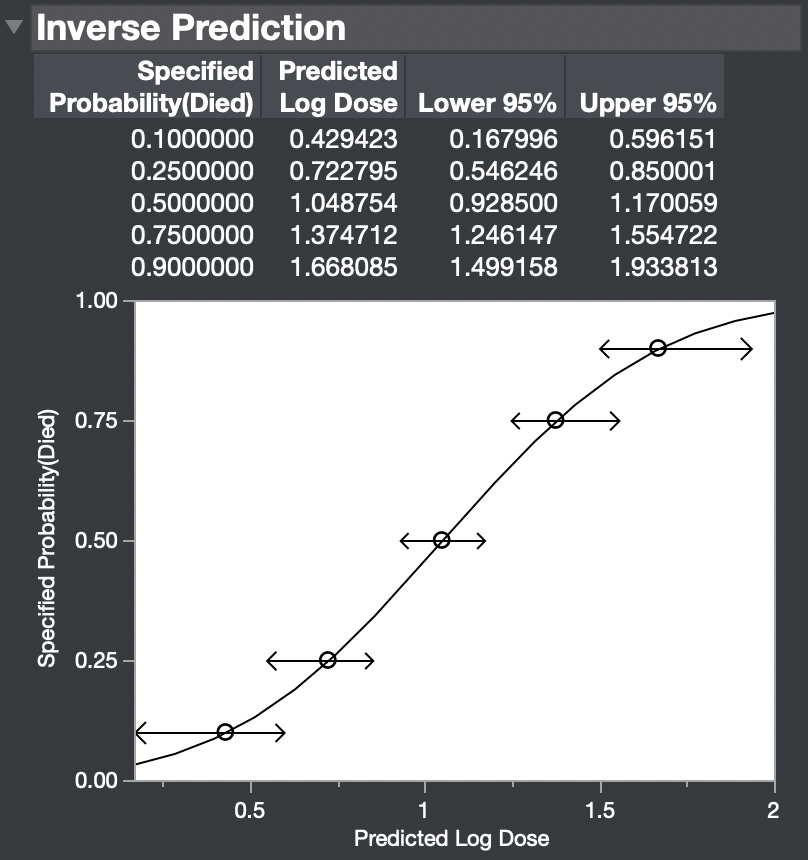
I forgot to add that there is an Inverse Prediction command available from the platform red triangle menu. In this example, I am asking for the Log Dose for several points from the CDF.
The result is:
Is this result what you are looking for?
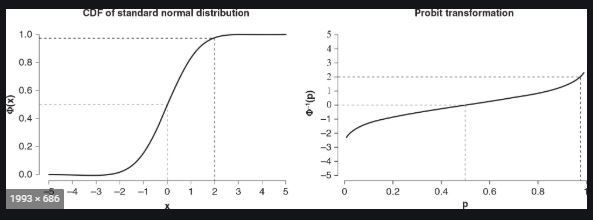
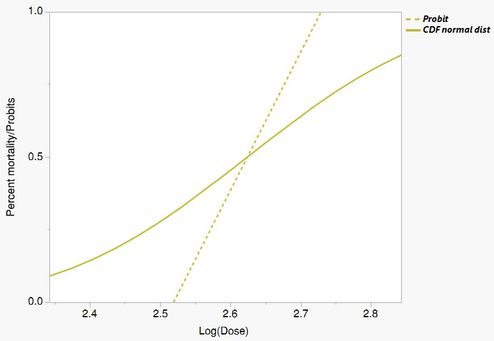
Sorry for being unclear in my initial question. I was trying to perform a probit transformation and convert the Y axis from a percentage (on the CDF of a normal distribuion: Φ(x)) into probits (the inverse of the CDF of a normal dist: Φ^-1(p)). See the snapshot from google below:
This is important for visualizing dose response for mortality, because the lethality of a toxicant in a population is not normally distributed (it is lognormal REF). Traditionally, toxicologists would convert percentage mortality into probits (See the 1952 Finney probit chart) prior to making a simple regression by hand, because it linearized the dose-response relationship (easier without computers). In my analysis previously mentioned, I account for this by employing the use of the probit link function. But the output is not in probits because it is predicted percent on a CDF normal dist. It is my understanding that this is the optimal way to visualize and compare dose response relationships between populations.
I did manage to figure out how to transform the Y of the predicted formulae into probits for visual purposes using:
Normal Quantile((Normal Distribution(Intercept+Slope*Log(dose))))
I merely needed to add an extra set of parenthesis!! I am confident because it gives me the same median lethal dose and linearizes the line:
In the above graph, I added .5 to the aforementioned formula because 0 probits= 50% mortality and by adding .5 they would intersect at the same median lethal dose.
You obviously know this stuff better than me, but I wanted to type it out to hopefully be of use to future users that might also want to transform the output into probits. Does this seem reasonable to you?
Many historical methods have been surpassed by superior methods when new theories, techniques, and technology become available. The older methods fade very slowly as we tend to hold on to anything that was successful in the past. Your results are correct, though, if you wish to pursue this approach.
I am not a toxicologist. I am a scientist, though, and a statistician. I would use the GLM as you have and include the population (e.g., Treatment) in the model. For example, let's extend my previous example:
Set up the model using the Fit Model launch dialog as before and include Treatment.
The Treatment effect will test an average difference (i.e., a unique intercept) indicating that one curve shifts left or right relative to the other curve. The Treatment * Log Dose effect will test a difference in the effect of Dose indicating a stronger or weaker transition between the asymptotes.
The regression plot in JMP clearly shows the two curves. The Effect Tests provide statistical evidence to decide about any difference between the curves. I don't see how a transformation will make this comparison more effective.
